《2025年智慧学堂九年级数学下册华师大版》

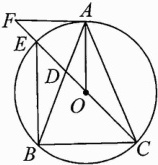
9. (2023福建中考)如图，已知△ABC内接于⊙O，CO的延长线交AB于点D，交⊙O于点E，交⊙O的切线AF于点F，且AF//BC.
(1)求证：AO//BE；
(2)求证：AO平分∠BAC.

答案： 证明:
(1)
∵AF是⊙O的切线，
∴AF⊥OA，∠OAF = 90°，
∵CE是⊙O的直径，
∴∠CBE = 90°，
∴∠OAF = ∠CBE，
∵AF//BC，
∴∠BAF = ∠ABC，
∴∠OAF - ∠BAF = ∠CBE - ∠ABC，即∠OAB = ∠ABE，
∴AO//BE。
(2)
∵∠ABE与∠ACE都是⌢EA所对的圆周角，
∴∠ABE = ∠ACE，
∵OA = OC，
∴∠ACE = ∠OAC，
∴∠ABE = ∠OAC，由
(1)知∠OAB = ∠ABE，
∴∠OAB = ∠OAC，
∴AO平分∠BAC。

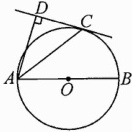
10. (甘孜州中考)如图，AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D.
(1)求证：∠CAD = ∠CAB；
(2)若$\frac{AD}{AB}$ = $\frac{2}{3}$，AC = 2$\sqrt{6}$，求CD的长.

答案：

(1)证明:连结OC，
∵CD是⊙O的切线，
∴OC⊥CD，
∵AD⊥CD，
∴AD//OC，
∴∠CAD = ∠ACO，
∵OA = OC，
∴∠CAO = ∠ACO，
∴∠CAD = ∠CAB；
(2)解:连结BC，
∵AD/AB = 2/3，
∴设AD = 2x，AB = 3x，
∵AB是⊙O的直径，
∴∠ACB = ∠ADC = 90°，
∵∠DAC = ∠CAB，
∴△ACD∽△ABC，
∴AD/AC = AC/AB，
∴2x/(2√6) = (2√6)/(3x)，
∴x = 2(负值舍去)，
∴AD = 4，
∴CD = √(AC² - AD²)=2√2。

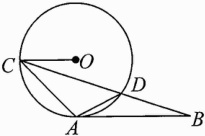
11. (2023南充中考)如图，AB与⊙O相切于点A，半径OC//AB，BC与⊙O相交于点D，连结AD.
(1)求证：∠OCA = ∠ADC；
(2)若AD = 2，tanB = $\frac{1}{3}$，求OC的长.

答案：

(1)证明:连结OA交BC于点F，
∵AB是⊙O的切线，
∴∠OAB = 90°，
∵OC//AB，
∴∠AOC = ∠OAB = 90°，
∵CO = OA，
∴∠OCA = 45°，
∴∠ADC = 1/2∠AOC = 45°，
∴∠OCA = ∠ADC；
(2)解:过点A作AE⊥BC于点E，
∵∠ADE = 45°，
∴△ADE是等腰直角三角形，
∴AE = DE = √2/2AD = √2，
∵tanB = AE/BE = 1/3，
∴BE = 3AE = 3√2，
∴AB = √(BE² + AE²)=√(18 + 2)=2√5，在Rt△ABF中，tanB = AF/AB = 1/3，
∴AF = 1/3AB = 2√5/3，
∵OC//AB，
∴∠OCF = ∠B，tan∠OCF = OF/OC = 1/3，设OC = r，则OF = OA - AF = r - 2√5/3，
∴3(r - 2√5/3)=r，解得r = √5，
∴OC = √5。

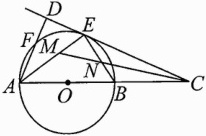
12. (2023宜宾中考)如图，以AB为直径的⊙O上有两点E、F，$\overset{\frown}{BE}=\overset{\frown}{EF}$，过点E作直线CD⊥AF交AF的延长线于点D，交AB的延长线于点C，过C作CM平分∠ACD交AE于点M，交BE于点N.
(1)求证：CD是⊙O的切线；
(2)求证：EM = EN；
(3)如果N是CM的中点，且AB = 9$\sqrt{5}$，求EN的长.

答案：

(1)证明:连结OE，
∵⌢BE = ⌢EF，
∴∠FAE = ∠EAB，
∵OA = OE，
∴∠AEO = ∠EAB，
∴∠FAE = ∠AEO，
∴AF//OE，
∵CD⊥AF，
∴OE⊥CD，
∵OE是⊙O的半径，
∴CD是⊙O的切线；
(2)证明:由
(1)知CD是⊙O的切线，易证∠CEB = ∠EAC，
∵CM平分∠ACD，
∴∠ECM = ∠ACM，
∴∠CEB + ∠ECM = ∠EAC + ∠ACM，
∴∠ENM = ∠EMN，
∴EM = EN；
(3)解:由
(2)知EM = EN，∠EMN = ∠ENM，
∵∠EMN = ∠BNC，
∴∠ECM = ∠BCN，
∴△EMC∽△BNC，
∴EM/BN = CE/CB = CM/CN，
∵N是CM的中点，
∴EM/BN = CE/CB = CM/CN = 2，
∴EM = 2BN，CE = 2BC，
∵∠BEC = ∠EAB，∠BCE = ∠ECA，
∴△BEC∽△EAC，
∴BE/EA = CE/CA = BC/EC = 1/2，
∴AE = 2BE，在Rt△ABE中，AE² + BE² = AB²，
∴(2BE)² + BE² = (9√5)²，
∴BE = 9，
∵EN = EM = 2BN，
∴EN = 2/3BE = 6，
∴EN的长为6。