2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. (玉林中考)小嘉说:将二次函数$y = x^2$的图象平移或翻折后经过点$(2,0)$有4种方法:①向右平移2个单位长度;②向右平移1个单位长度,再向下平移1个单位长度;③向下平移4个单位长度;④沿$x$轴翻折,再向上平移4个单位长度. 你认为小嘉说的方法中正确的有( )
A. 1种
B. 2种
C. 3种
D. 4种
A. 1种
B. 2种
C. 3种
D. 4种
答案:
D
11. (衢州中考)已知二次函数$y = a(x - 1)^2 - a$($a \neq 0$),当$- 1 \leq x \leq 4$时,$y$的最小值为$- 4$,则$a$的值为( )
A. $\frac{1}{2}$或4
B. $\frac{4}{3}$或$-\frac{1}{2}$
C. $-\frac{4}{3}$或4
D. $-\frac{1}{2}$或4
A. $\frac{1}{2}$或4
B. $\frac{4}{3}$或$-\frac{1}{2}$
C. $-\frac{4}{3}$或4
D. $-\frac{1}{2}$或4
答案:
D
12. 已知抛物线$y = - 4(x + m)^2 + 2$,当$x \geq 1$时,$y$随$x$的增大而减小,那么$m$的取值范围是__________.
答案:
$m = - 1$
13. (苏州高新区月考)下列关于二次函数$y = -(x - m)^2 + m^2 + 1$($m$为常数)的结论:①该函数的图象与函数$y = - x^2$的图象形状相同;②该函数的图象一定经过点$(0,1)$;③当$x > 0$时,$y$随$x$的增大而减小;④该函数的图象的顶点在函数$y = x^2 + 1$的图象上. 其中所有正确结论的序号是__________.
答案:
①②④
14. 如图,直线$y = n$与二次函数$y = \frac{1}{2}(x - 2)^2 - 1$的图象交于点$B$、点$C$,二次函数的图象的顶点为$A$,当$\triangle ABC$是等腰直角三角形时,$n =$______.
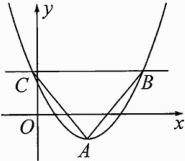

答案:
1
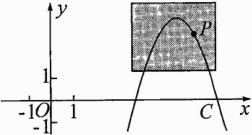
15. (河北中考)如图,点$P(a,3)$在抛物线$C:y = 4 - (6 - x)^2$上,且在$C$的对称轴右侧.
(1)写出$C$的对称轴和$y$的最大值,并求$a$的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点$P$及$C$的一段,分别记为$P'$,$C'$. 平移该胶片,使$C'$所在抛物线对应的函数解析式恰为$y = - x^2 + 6x - 9$. 求点$P'$移动的最短路程.
(1)写出$C$的对称轴和$y$的最大值,并求$a$的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点$P$及$C$的一段,分别记为$P'$,$C'$. 平移该胶片,使$C'$所在抛物线对应的函数解析式恰为$y = - x^2 + 6x - 9$. 求点$P'$移动的最短路程.

答案:
解:
(1)
∵抛物线$C:y = 4-(x - 6)^2 = -(x - 6)^2 + 4$,
∴抛物线的对称轴为直线$x = 6$,$y$的最大值为4。当$y = 3$时,$3 = 4-(x - 6)^2$,解得$x_1 = 5$,$x_2 = 7$,
∵点$P(a,3)$在对称轴的右侧,
∴$a > 6$,
∴$a = 7$。
(2)
∵平移后的抛物线的解析式为$y = - x^2 + 6x - 9 = -(x - 3)^2$,
∴平移后抛物线的顶点坐标为$(3,0)$,易知平移前抛物线的顶点坐标为$(6,4)$,
∴点$P'$移动的最短路程为$\sqrt{(6 - 3)^2+(4 - 0)^2}=5$。
(1)
∵抛物线$C:y = 4-(x - 6)^2 = -(x - 6)^2 + 4$,
∴抛物线的对称轴为直线$x = 6$,$y$的最大值为4。当$y = 3$时,$3 = 4-(x - 6)^2$,解得$x_1 = 5$,$x_2 = 7$,
∵点$P(a,3)$在对称轴的右侧,
∴$a > 6$,
∴$a = 7$。
(2)
∵平移后的抛物线的解析式为$y = - x^2 + 6x - 9 = -(x - 3)^2$,
∴平移后抛物线的顶点坐标为$(3,0)$,易知平移前抛物线的顶点坐标为$(6,4)$,
∴点$P'$移动的最短路程为$\sqrt{(6 - 3)^2+(4 - 0)^2}=5$。
16. 抛物线$y = (x - 1)^2 - 4$与$x$轴交于$A$,$B$两点(点$A$在点$B$左侧),与$y$轴交于点$C$,点$P$为第四象限的抛物线上的一点,且$\angle PCB + \angle CAB = 135^{\circ}$.
(1)求$\triangle ABC$的面积;
(2)求证:$\angle ACB = \angle BCP$;
(3)求点$P$的坐标.
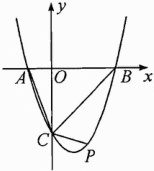
(1)求$\triangle ABC$的面积;
(2)求证:$\angle ACB = \angle BCP$;
(3)求点$P$的坐标.

答案:
(1)解:$S_{\triangle ABC}=\frac{1}{2}\times4\times3 = 6$;
(2)证明:$B(3,0)$,$C(0,-3)$,
∴$OB = OC$,
∴$\angle ABC = 45^{\circ}$,$\angle BAC = 135^{\circ}$,又$\angle BCP+\angle CAB = 135^{\circ}$,
∴$\angle ACB=\angle BCP$;
(3)解:过点$B$作$BS\perp x$轴,交$CP$的延长线于点$S$,由
(2)知$\angle ABC=\angle SBC$,$\angle ACB=\angle BCP$,又$\because BC = BC$,$\therefore\triangle ABC\cong\triangle SBC$,$\therefore AB = SB = 4$,$\therefore S(3,-4)$,$\therefore l_{BC}:y = -\frac{1}{3}x - 3$,联立$\begin{cases}y = -\frac{1}{3}x - 3\\y = x^2 - 2x - 3\end{cases}$,得$P(\frac{5}{3},-\frac{32}{9})$。
(1)解:$S_{\triangle ABC}=\frac{1}{2}\times4\times3 = 6$;
(2)证明:$B(3,0)$,$C(0,-3)$,
∴$OB = OC$,
∴$\angle ABC = 45^{\circ}$,$\angle BAC = 135^{\circ}$,又$\angle BCP+\angle CAB = 135^{\circ}$,
∴$\angle ACB=\angle BCP$;
(3)解:过点$B$作$BS\perp x$轴,交$CP$的延长线于点$S$,由
(2)知$\angle ABC=\angle SBC$,$\angle ACB=\angle BCP$,又$\because BC = BC$,$\therefore\triangle ABC\cong\triangle SBC$,$\therefore AB = SB = 4$,$\therefore S(3,-4)$,$\therefore l_{BC}:y = -\frac{1}{3}x - 3$,联立$\begin{cases}y = -\frac{1}{3}x - 3\\y = x^2 - 2x - 3\end{cases}$,得$P(\frac{5}{3},-\frac{32}{9})$。
查看更多完整答案,请扫码查看


