2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
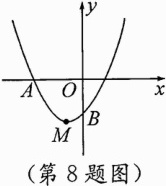
8. (2023宜宾中考)如图,抛物线$y = ax^2 + bx + c$经过点$A(-3,0)$,顶点为$M(-1,m)$,且抛物线与$y$轴的交点$B$在$(0,-2)$与$(0,-3)$之间(不含端点),则下列结论:①当$-3\leqslant x\leqslant1$时,$y\leqslant0$;②当$\triangle ABM$的面积为$\frac{3\sqrt{3}}{2}$时,$a = \frac{\sqrt{3}}{2}$;③当$\triangle ABM$为直角三角形时,在$\triangle AOB$内存在唯一一点$P$,使得$PA + PO + PB$的值最小,最小值的平方为$18 + 9\sqrt{3}$. 其中正确的结论是________.(填写所有正确结论的序号)

答案:
①②
9. (2023南充中考)某工厂计划从$A$,$B$两种产品中选择一种生产并销售,每日产销$x$件,已知$A$产品成本价$m$元/件($m$为常数),且$4\leqslant m\leqslant6$,售价$8$元/件,每日最多产销$500$件,同时每日共支付专利费$30$元;$B$产品成本价$12$元/件,售价$20$元/件,每日最多产销$300$件,同时每日支付专利费$y$元,$y$(元)与每日产销$x$(件)满足关系式$y = 80 + 0.01x^2$.
(1)若产销$A$,$B$两种产品的日利润分别为$w_1$元,$w_2$元,请分别写出$w_1$,$w_2$与$x$的函数关系式,并写出$x$的取值范围;
(2)分别求出产销$A$,$B$两种产品的最大日利润.($A$产品的最大日利润用含$m$的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.
【利润 =(售价 - 成本)×产销数量 - 专利费】
(1)若产销$A$,$B$两种产品的日利润分别为$w_1$元,$w_2$元,请分别写出$w_1$,$w_2$与$x$的函数关系式,并写出$x$的取值范围;
(2)分别求出产销$A$,$B$两种产品的最大日利润.($A$产品的最大日利润用含$m$的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.
【利润 =(售价 - 成本)×产销数量 - 专利费】
答案:
解:
(1)根据题意,得$w_{1}=(8 - m)x - 30(0\leqslant x\leqslant500)$,$w_{2}=-0.01x^{2}+8x - 80(0\leqslant x\leqslant300)$;
(2)$\because8 - m>0$,$\therefore w_{1}$随$x$的增大而增大,又$0\leqslant x\leqslant500$,$\therefore$当$x = 500$时,$w_{1}$有最大值,即$w_{1最大}=-500m + 3970$(元),$\because w_{2}=-0.01x^{2}+8x - 80=-0.01(x - 400)^{2}+1520$,又$\because - 0.01<0$,对称轴$x = 400$,$\therefore$当$0\leqslant x\leqslant300$时,$w_{2}$随$x$的增大而增大,$\therefore$当$x = 300$时,$w_{2最大}=-0.01\times(300 - 400)^{2}+1520 = 1420$(元);
(3)①若$w_{1最大}=w_{2最大}$,即$-500m + 3970 = 1420$,解得$m = 5.1$,②若$w_{1最大}>w_{2最大}$,即$-500m + 3970>1420$,解得$m<5.1$,③若$w_{1最大}<w_{2最大}$,即$-500m + 3970<1420$,解得$m>5.1$,又$4\leqslant m\leqslant6$,综上可得,为获得最大日利润:当$m = 5.1$时,选择$A$,$B$产品产销均可;当$4\leqslant m<5.1$时,选择$A$产品产销;当$5.1<m\leqslant6$时,选择$B$产品产销。答:当$A$产品成本价为$5.1$元时,工厂选择$A$或$B$产品产销日利润一样;当$A$产品成本价$4\leqslant m<5.1$时,工厂选择$A$产品产销日利润最大;当产品成本价$5.1<m\leqslant6$时,工厂选择$B$产品产销日利润最大。
(1)根据题意,得$w_{1}=(8 - m)x - 30(0\leqslant x\leqslant500)$,$w_{2}=-0.01x^{2}+8x - 80(0\leqslant x\leqslant300)$;
(2)$\because8 - m>0$,$\therefore w_{1}$随$x$的增大而增大,又$0\leqslant x\leqslant500$,$\therefore$当$x = 500$时,$w_{1}$有最大值,即$w_{1最大}=-500m + 3970$(元),$\because w_{2}=-0.01x^{2}+8x - 80=-0.01(x - 400)^{2}+1520$,又$\because - 0.01<0$,对称轴$x = 400$,$\therefore$当$0\leqslant x\leqslant300$时,$w_{2}$随$x$的增大而增大,$\therefore$当$x = 300$时,$w_{2最大}=-0.01\times(300 - 400)^{2}+1520 = 1420$(元);
(3)①若$w_{1最大}=w_{2最大}$,即$-500m + 3970 = 1420$,解得$m = 5.1$,②若$w_{1最大}>w_{2最大}$,即$-500m + 3970>1420$,解得$m<5.1$,③若$w_{1最大}<w_{2最大}$,即$-500m + 3970<1420$,解得$m>5.1$,又$4\leqslant m\leqslant6$,综上可得,为获得最大日利润:当$m = 5.1$时,选择$A$,$B$产品产销均可;当$4\leqslant m<5.1$时,选择$A$产品产销;当$5.1<m\leqslant6$时,选择$B$产品产销。答:当$A$产品成本价为$5.1$元时,工厂选择$A$或$B$产品产销日利润一样;当$A$产品成本价$4\leqslant m<5.1$时,工厂选择$A$产品产销日利润最大;当产品成本价$5.1<m\leqslant6$时,工厂选择$B$产品产销日利润最大。
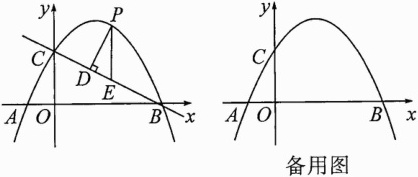
10. (2023重庆中考A卷)如图,在平面直角坐标系中,抛物线$y = ax^2 + bx + 2$过点$(1,3)$,且交$x$轴于$A(-1,0)$,$B$两点,交$y$轴于点$C$.
(1)求抛物线的表达式;
(2)点$P$是直线$BC$上方抛物线上的一动点,过点$P$作$PD\perp BC$于点$D$,过点$P$作$y$轴的平行线交直线$BC$于点$E$,求$\triangle PDE$周长的最大值及此时点$P$的坐标;
(3)在(2)中$\triangle PDE$周长取得最大值的条件下,将该抛物线沿射线$CB$方向平移$\sqrt{5}$个单位长度,点$M$为平移后的抛物线的对称轴上一点. 在平面内确定一点$N$,使得以点$A$,$P$,$M$,$N$为顶点的四边形是菱形,写出所有符合条件的点$N$的坐标,并写出求解点$N$的坐标的其中一种情况的过程.
(1)求抛物线的表达式;
(2)点$P$是直线$BC$上方抛物线上的一动点,过点$P$作$PD\perp BC$于点$D$,过点$P$作$y$轴的平行线交直线$BC$于点$E$,求$\triangle PDE$周长的最大值及此时点$P$的坐标;
(3)在(2)中$\triangle PDE$周长取得最大值的条件下,将该抛物线沿射线$CB$方向平移$\sqrt{5}$个单位长度,点$M$为平移后的抛物线的对称轴上一点. 在平面内确定一点$N$,使得以点$A$,$P$,$M$,$N$为顶点的四边形是菱形,写出所有符合条件的点$N$的坐标,并写出求解点$N$的坐标的其中一种情况的过程.

答案:
解:
(1)$y = -\frac{1}{2}x^{2}+\frac{3}{2}x + 2$;
(2)$\triangle PDE$周长的最大值为$\frac{10 + 6\sqrt{5}}{5}$,此时点$P$的坐标为$(2,3)$;
(3)点$N$的坐标为$(\frac{1}{2},\frac{3\sqrt{7}}{2})$或$(\frac{1}{2},-\frac{3\sqrt{7}}{2})$或$(-\frac{5}{2},-\frac{9}{2})$。过程略。
(1)$y = -\frac{1}{2}x^{2}+\frac{3}{2}x + 2$;
(2)$\triangle PDE$周长的最大值为$\frac{10 + 6\sqrt{5}}{5}$,此时点$P$的坐标为$(2,3)$;
(3)点$N$的坐标为$(\frac{1}{2},\frac{3\sqrt{7}}{2})$或$(\frac{1}{2},-\frac{3\sqrt{7}}{2})$或$(-\frac{5}{2},-\frac{9}{2})$。过程略。
查看更多完整答案,请扫码查看


