2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列条件中,能确定圆的是 ( )
A. 以点O为圆心
B. 以2cm为半径
C. 以点O为圆心,5cm为半径
D. 经过已知点A
A. 以点O为圆心
B. 以2cm为半径
C. 以点O为圆心,5cm为半径
D. 经过已知点A
答案:
C
2. 下面四个图中的角,是圆心角的是 ( )
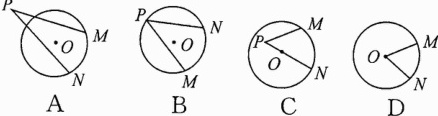

答案:
D
3. 过圆上一点可以作出圆的最长弦的条数为 ( )
A. 1条
B. 2条
C. 3条
D. 无数条
A. 1条
B. 2条
C. 3条
D. 无数条
答案:
A
4. 下列命题中正确的有 ( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A. 1个
B. 2个
C. 3个
D. 4个
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A. 1个
B. 2个
C. 3个
D. 4个
答案:
A
5. 如图,在⊙O中,若点A,O,D,点C,D,E以及点B,O,C分别在一条直线上,则图中的弦有 ( )
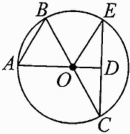
A. 2条
B. 3条
C. 4条
D. 5条

A. 2条
B. 3条
C. 4条
D. 5条
答案:
B
6.(2023雅礼实验中学模拟)如图,A,B,C都是⊙O上的点,且点A,O,B在同一条直线上,连接OC,AC.
(1)指出图中的半径与直径;
(2)指出图中的弦、弧、优弧.
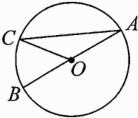
(1)指出图中的半径与直径;
(2)指出图中的弦、弧、优弧.

答案:
解:
(1)图中的半径有3条,分别是OA,OB,OC;直径有1条,是AB;
(2)图中的弦有2条,分别是AC,AB;弧有6条,分别是$\overset{\frown}{AC}$,$\overset{\frown}{ACB}$,$\overset{\frown}{AB}$,$\overset{\frown}{BC}$,$\overset{\frown}{ABC}$,$\overset{\frown}{CAB}$;优弧有2条,分别是$\overset{\frown}{CAB}$,$\overset{\frown}{ABC}$.
(1)图中的半径有3条,分别是OA,OB,OC;直径有1条,是AB;
(2)图中的弦有2条,分别是AC,AB;弧有6条,分别是$\overset{\frown}{AC}$,$\overset{\frown}{ACB}$,$\overset{\frown}{AB}$,$\overset{\frown}{BC}$,$\overset{\frown}{ABC}$,$\overset{\frown}{CAB}$;优弧有2条,分别是$\overset{\frown}{CAB}$,$\overset{\frown}{ABC}$.
7.(2023云南中考)如图,AB是⊙O的直径,C是⊙O上一点,若∠BOC = 66°,则∠A = ( )
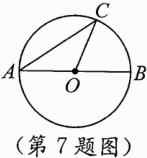
A. 66°
B. 33°
C. 24°
D. 30°

A. 66°
B. 33°
C. 24°
D. 30°
答案:
B
8. 如图,AB是⊙O的直径,AC为弦,OD//BC并交AC于D,且OD = 2cm,则BC的长为________cm.
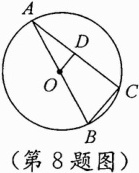

答案:
4
9. 如图,在⊙O中,D、E分别为半径OA、OB上的点,且AD = BE,点C为弧AB上一点,连结CD、CE、CO,∠AOC = ∠BOC. 求证:CD = CE.
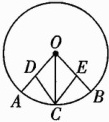

答案:
证明:
∵OA=OB,AD=BE,
∴OD=OE,在△DOC和△EOC中,OD=OE,∠AOC=∠BOC,OC=OC,
∴△DOC≌△EOC,
∴CD=CE.
∵OA=OB,AD=BE,
∴OD=OE,在△DOC和△EOC中,OD=OE,∠AOC=∠BOC,OC=OC,
∴△DOC≌△EOC,
∴CD=CE.
10. 如图所示,AB、AC为⊙O的弦,连结CO、BO并延长分别交弦AB、AC于点E、F,∠B = ∠C. 求证:CE = BF.
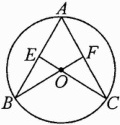

答案:
证明:在△OBE与△OCF中,$\begin{cases}\angle B=\angle C,\\OB=OC,\\\angle BOE=\angle COF,\end{cases}$
∴△OBE≌△OCF,
∴OE=OF,
∴OE+OC=OF+OB,即CE=BF.
∴△OBE≌△OCF,
∴OE=OF,
∴OE+OC=OF+OB,即CE=BF.
查看更多完整答案,请扫码查看


