《2025年小学学霸作业本六年级数学下册人教版广东专版》

1. 造纸术是我国四大发明之一。小峰在家做造纸的实验，若做4张纸用了5g明胶，则做同样的10张纸，需要用多少克明胶？
(1)分析：由“同样的”可知每张纸需要用的(明胶)的质量一定，而纸的张数与明胶的质量(是)两种相关联的量(填“是”或“不是”)，故明胶的质量与纸的张数成(正)比例关系。“5 : 4”表示的是(每张纸需要明胶的质量)。

答案： 明胶@@是@@正@@每张纸需用多少克明胶

(2)设需要用$x$g明胶，列比例为：($5:4 = x:10$)，解得$x=$(12.5)。

答案： $5:4 = x:10$@@12.5

2. [新趋势·学科融合]成语“立竿见影”在《辞源》里的解释为“竿立而影现，喻收效迅速”。用数学的眼光看，是应用了比例的关系。小兰在同一时间、同一地点测量一排树的高度和影长。根据表格完成下列各题。
(1)树高和影长两种量成(正)比例关系。

(2)当小兰测得一棵树的影长是3.2m时，这棵树高多少米？(用比例解)

答案： 正@@解：设这棵树高$x$m。 $20:8 = x:3.2$ 解得$x = 8$ 答：这棵树高8 m。

3. [新情境·科技成就]我国科学家自主研发的“北脑二号”填补了国内高性能侵入式脑机接口的空白。一台脑机接口设备解码50个词语，其中正确的有38个，按此正确率，再解码75个词语，正确的共有多少个？(用比例解)

答案： 解：设正确的共有$x$个。 $38:50 = x:(50 + 75)$ 解得$x = 95$ 答：正确的共有95个。

4. 某地将电力线路由地面上架空改为电缆敷(fū)设入地。某路段960m的线路，6天改完了288m，照这样的速度，还要多少天可以改完？(用比例解)

答案： 解：设还要$x$天可以改完。 $288:6=(960 - 288):x$ 解得$x = 14$ 答：还要14天可以改完。

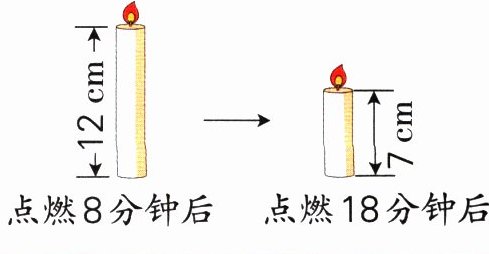
5. 假设蜡烛每分钟燃烧的长度一定。蜡烛最初的长度是多少厘米？

答案：  解：设蜡烛最初的长度是$x$cm。 $(x - 12):8=(x - 7):18$ 解得$x = 16$ 答：蜡烛最初的长度是16 cm。 解析：根据“蜡烛每分钟燃烧的长度一定”可知蜡烛燃烧的长度与燃烧的时间成正比例关系，又燃烧的长度等于蜡烛最初的长度减去剩下的长度，据此列方程解答即可。