《2025年小学学霸作业本六年级数学下册人教版广东专版》

1. 在下面图形中，以任意一边所在直线为轴旋转一周都可以得到圆柱的是( )。.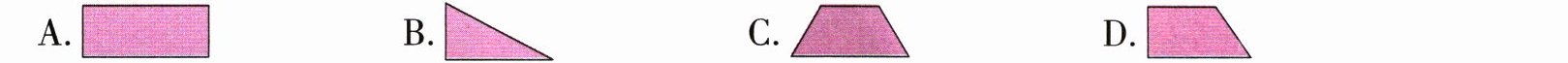

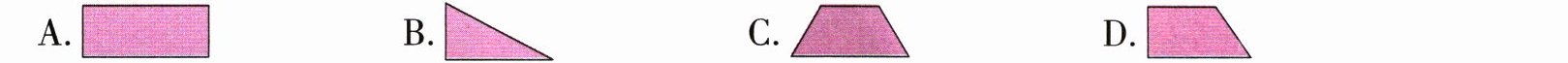
答案： A

2. (揭阳期末真题)一个圆柱的侧面展开图是正方形，这个圆柱的底面半径与高的比是( )。
A. 1 : π
B. π : 1
C. 1 : (2π)
D. (2π) : 1

答案： C

3. 压路机的前轮是圆柱形，前轮横截面的半径是0.5 m，长是1.6 m。如果这个压路机以每分钟转动12圈的速度前进，每分钟压路的面积是( )m²。(得数保留一位小数)

答案： 60.3

4. 一块长方形铁皮长18.84 dm，宽6 dm，用这块铁皮卷成一个圆柱形铁皮水桶的侧面，另配一个底面制成一个最大的水桶，这个铁皮水桶的表面积是多少平方分米？水桶的容积是多少？(铁皮厚度、接头处不计)

答案： 当以长为底面周长时，水桶最大。 18.84÷3.14÷2 = 3(dm) 18.84×6 + 3.14×3² = 141.3(dm²) 3.14×3²×6 = 169.56(dm³)=169.56(L) 答：这个铁皮水桶的表面积是141.3 dm²，水桶的容积是169.56 L。

5. 一个棱长是5 dm的正方体容器装满水后，将水倒入一个底面积是25 dm²的圆锥形容器里，正好装满，这个圆锥形容器的高是多少分米？(容器厚度不计)

答案： 5×5×5 = 125(dm³) 125×3÷25 = 15(dm) 答：这个圆锥形容器的高是15 dm。

6. 一个圆柱和一个圆锥的底面半径相等，高也相等，圆锥的体积是30 cm³，圆柱的体积是( )cm³。
A. 10
B. 30
C. 45
D. 90

答案： D

7. 苏苏把一块体积是1 dm³的橡皮泥捏成一个圆柱形模型和一个与圆柱形模型底面积相等、高也相等的圆锥形模型，圆柱形模型和圆锥形模型的体积之比是多少？捏成的圆锥形模型的体积是多少立方分米？

答案： （解法不唯一）1 : 1/3 = 3 : 1 1÷(3 + 1)×1 = 0.25(dm³) 答：圆柱形模型和圆锥形模型的体积之比是3 : 1。捏成的圆锥形模型的体积是0.25 dm³。 解析：根据圆柱和圆锥的体积计算公式可知，等底、等高的圆柱和圆锥的体积之比为1 : 1/3 = 3 : 1，又知圆柱和圆锥的体积之和，可用按比分配的方法求出圆锥的体积。解法不唯一，合理即可。