《2025年小学学霸作业本六年级数学下册人教版广东专版》

1. 下面每题中的两种量是否成正比例关系？是的在括号里画“√”，反之画“×”。
(1)打字时间一定，总字数和速度。( ) (2)正方体的棱长与棱长和。( )
(3)看一本书，已看页数和未看页数。( )(4)圆的面积和它的半径。 ( )

答案： √@@√@@×@@×

2. $A$和$B$成正比例关系，当$A = 1.2$时，$B = 6$，当$A = 0.6$时，$B = (\ \ \ \ )$。
A. $0.3$
B. $0.12$
C. $12$
D. $3$

答案： 3

3. [新趋势·学科融合]一个小组做探究弹簧的伸长量(在一定的弹性极限内)与所受拉力大小的关系实验，记录的数据如下表所示。

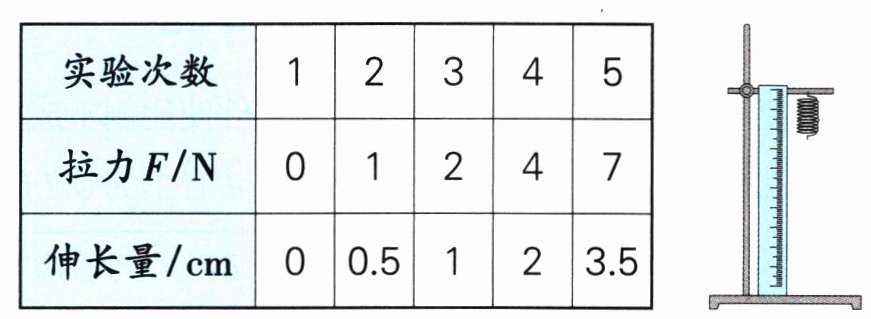
(1)写出3组拉力与伸长量的比：( )，( )，( )，拉力与伸长量的比的比值都是( )，这个比值表示( )。
(2)拉力与伸长量成( )比例关系，理由：________________________。
(3)在上面右图中描出拉力与对应的伸长量的点，按顺序连起来并延长。观察图象，发现它的特点：( )。
(4)不计算，根据图象判断，拉力为$6N$时，弹簧的伸长量是( )cm。弹簧的伸长量是$1.5cm$时，拉力是( )N(牛顿)。

答案： 1 : 0.5@@2 : 1@@7 : 3.5@@2@@弹簧的伸长量与拉力的关系@@正@@拉力与伸长量的比值是一个定值@@F/N 8| 6| 4| 2| 0| 1 2 3 4 伸长量/cm 是从(0,0)出发的无限延伸的射线@@3@@3

4. 石英石硬度较高、色彩多样。下表是关于正方体石英石的一些数据，哪两种量成正比例关系？说明理由并将下表补充完整。

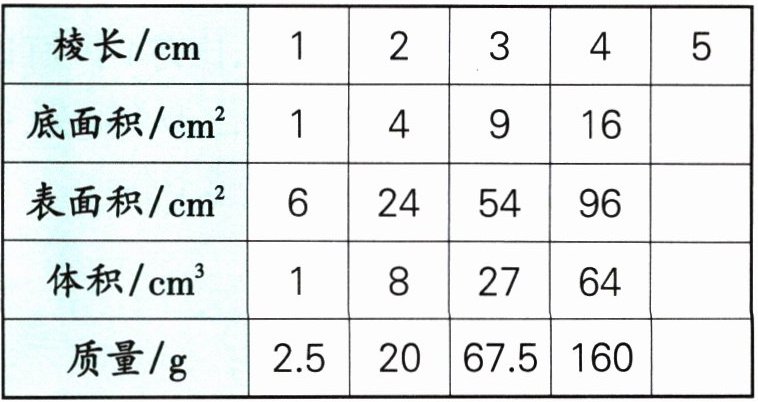
答案： （从上到下）25@@150@@125@@312.5@@表面积与底面积成正比例关系，因为表面积与底面积是两种相关联的量，且表面积÷底面积 = 6(定值)；质量与体积成正比例关系，因为质量与体积是两种相关联的量，且质量÷体积 = 2.5(定值)。解析：要判断两种量是否成正比例关系，就要看这两种量是否符合成正比例关系的两个条件：
(1)两种量是两种相关联的量；
(2)两种量中相对应的两个数的比值一定。正方体的底面积 = 棱长×棱长，表面积 = 底面积×6，体积 = 棱长×棱长×棱长，据此计算并判断是否成正比例关系即可。