《2025年小学学霸作业本六年级数学下册人教版广东专版》

1. “转化”是常用的数学思想方法。如图，把圆柱转化成长方体。若圆柱的底面半径是5 cm，高是10 cm，则长方体的长是( )cm，宽是( )cm，体积是( )$cm^{3}$。

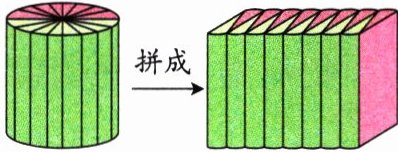
答案： 15.7@@5@@785

2. (佛山期末真题)如图，一卷卷筒纸的纸厚是3 cm，如果每立方厘米纸的质量是0.25 g，那么这卷卷筒纸的质量是多少克?

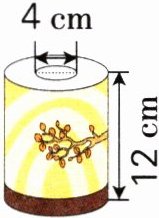
答案： 4÷2 = 2(cm) 2 + 3 = 5(cm) 3.14×(5² - 2²)×12×0.25 = 197.82(g) 答：这卷卷筒纸的质量是197.82(g)。

3. [新情境·人文景观]北京天坛的祈年殿内有28根金丝楠木大木柱，内围的4根“龙井柱”(圆柱形)象征春、夏、秋、冬，每根的高约是20 m，底面直径是1.2 m，这4根“龙井柱”约用多少立方米金丝楠木?

答案： 3.14×(1.2÷2)²×20×4 = 90.432(m³) 答：这4根“龙井柱”约用90.432 m³金丝楠木。

4. [新趋势·材料阅读]学习了圆柱的体积之后，聪聪做了一个实验，步骤如下。
第一步：在一个底面半径是2 dm、高是4 dm的圆柱形容器甲中注满水。
第二步：将一根底面半径是10 cm、高是48 cm的铁棒垂直放入容器甲中，水溢出。
第三步：取出铁棒，再将一块铁块放入容器甲中，测量得此时水面高3.5 dm。
第四步：往一个底面直径是5 dm的圆柱形容器乙中倒入一点水。
第五步：将容器甲中的铁块取出放到容器乙中，水没过铁块但未溢出。
(1)第二步实验结束时，溢出的水的体积是( )$dm^{3}$。
(2)放入铁块后，容器乙中的水面上升了多少厘米?

答案： 12.56@@解析：48 cm = 4.8 dm，4.8＞4，所以这根铁棒在水中部分的形状是一个底面半径是10 cm、高是4 dm的圆柱，这个圆柱的体积就是溢出水的体积。注意单位统一。10 cm = 1 dm，3.14×1²×4 = 12.56(dm³)。
(2)12.56÷(3.14×2²)=1(dm) 4 - 1 = 3(dm) 铁块体积：3.14×2²×(3.5 - 3)=6.28(dm³) 6.28÷[3.14×(5÷2)²]=0.32(dm) 0.32 dm = 3.2 cm 答：容器乙中的水面上升了3.2 cm。 解析：先求出取出铁棒后，容器甲中的水面高度，再放入铁块，此时水面上升部分的体积即为铁块的体积，最后用铁块的体积除以容器乙的底面积，即为容器乙中水面上升的高度。

5. 一根圆柱形木块平均切成三块(如图1)，表面积增加了50.24 $cm^{2}$；平均切成四块(如图2)，表面积增加了192 $cm^{2}$。这根圆柱形木块的体积是多少立方厘米?

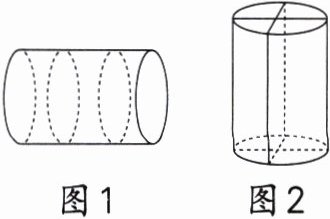
答案： 50.24÷2÷2 = 12.56(cm²) 解：设圆柱的底面半径为r cm。 3.14r² = 12.56 r² = 4 r = 2 192÷2÷2÷(2×2)=12(cm) 12.56×12 = 150.72(cm³) 答：这根圆柱形木块的体积是150.72 cm³。 解析：圆柱形木块平均切成三块，表面积增加了2×2 = 4(个)底面积；平均切成四块，表面积增加了2×2 = 4(个)以圆柱底面直径为宽、以圆柱高为长的长方形的面积，据此求出圆柱的底面半径和高，再求体积。