《2025年小学学霸作业本六年级数学下册人教版广东专版》

5. 一根长是1 m、底面直径是20 cm的圆柱形木头浮在水面上，小明发现它正好有一半露出水面，请你求出这根木头与水接触的面积。

答案： 1 m = 100 cm 20÷2 = 10(cm) 3.14×10²×2÷2 + 3.14×20×100÷2 = 3454(cm²) 答：这根木头与水接触的面积是3454 cm²。

6. [教材改编]某公园有一些生肖石柱，每个石柱都是由一个圆柱和一个正方体组成的(如图)。关于这些石柱，已知如下信息。
①每个石柱下方正方体的棱长为3 m。
②每个石柱上方圆柱的底面直径为2 m，高为10 m。
③公园一共有12个生肖石柱。
④石柱表面做了封蜡保护，每平方米用0.2 L蜡。(不包括下底面)
每个石柱用了多少升蜡？解决本题需用的信息是( )(填序号)，列式解答。

答案： ①②④@@3.14×2×10 + 3×3×5 = 107.8(m²) 107.8×0.2 = 21.56(L) 答：每个石柱用了21.56 L蜡。

7. 如图，一个圆柱截去10 cm后，表面积减少了157 cm²，原来圆柱的表面积是多少平方厘米？

答案： 157÷10 = 15.7(cm) 15.7÷3.14÷2 = 2.5(cm) 15.7×(10 + 12)+3.14×2.5²×2 = 384.65(cm²) 答：原来圆柱的表面积是384.65 cm²。 解析：表面积减少的是高为10 cm的圆柱的侧面积，用减少的面积除以10 cm求出底面周长，进而求出底面半径，然后根据“圆柱表面积 = 侧面积+底面积×2”求解即可。

8. [新趋势·思维探究]如图，一个底面半径为5 dm、高为8 dm的圆柱，可以横着切成两块，也可以竖着切成两块。怎样切成两块后的表面积更大？
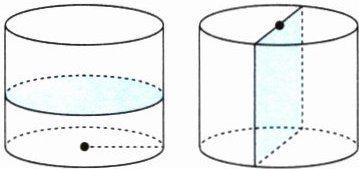
(1)下面是成成的思考过程，请你帮他补充完整。
成成：要想知道怎样切成两块后的表面积更大，因为圆柱的表面积不变，所以只需判断怎样切增加的表面积更大即可。
①横着切成两块，增加的表面积=圆柱的( )×( )。
②竖着切成两块，增加的表面积=( )的面积×( )，其中长方形的宽为( )dm，长为( )dm。
(2)请你列式计算。

答案： 底面积@@2@@长方形@@2@@8@@10@@3.14×5²×2 = 157(dm²) 10×8×2 = 160(dm²) 157＜160 答：竖着切成两块后的表面积更大。 解析：注意分清不同的切块方式形成的截面是什么形状，再分别计算出增加的截面的面积，最后比较大小得出结论。