《2025年小学学霸作业本六年级数学下册人教版广东专版》

1. 填空。
(1)(珠海期末真题)如右图，把直角三角形ABC沿着边AB旋转一周，得到的立体图形是( )，它的体积是( )cm³。

答案： 圆锥@@56.52

(2)一个圆锥的体积是76 cm³，底面积是19 cm²，则高是( )cm。

答案： 12

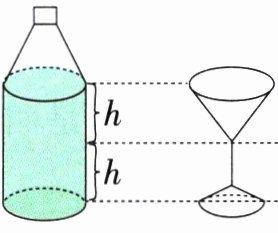
2. 如右图，瓶底的面积和锥形杯杯口的面积相等，将瓶子中的液体倒入锥形杯子中，能倒满( )杯。


A. 3
B. 4
C. 6
D. 9

答案： C

3. 求下面各图形的体积。

答案： $\frac{1}{3}×40×12 = 160(cm^{3})$@@$\frac{1}{3}×3.14×2^{2}×4.5 = 18.84(dm^{3})$@@$\frac{1}{3}×3.14×(6÷2)^{2}×4.5 = 42.39(dm^{3})$

4. [新情境·数学文化]《九章算术》中有一题：“今有圆锥，下周三丈五尺，高五丈一尺，问积几何？”其意思为“有圆锥，底面周长三丈五尺，高五丈一尺，求体积。”则此圆锥的体积为多少立方尺？(古制1丈=10尺，圆周率π取3)

答案： 三丈五尺 = 35 尺 五丈一尺 = 51 尺 $\frac{1}{3}×3×(35÷3÷2)^{2}×51 = 1735\frac{5}{12}$(立方尺) 答：此圆锥的体积为$1735\frac{5}{12}$立方尺。

5. [教材改编]某地公路局近期对各道路进行了整修。一个圆锥形沙堆，底面积是9.42 m²，高是0.9 m，把这堆沙子铺入长4.5 m、宽2 m的长方体沙坑里，可以铺多厚？

答案： $\frac{1}{3}×9.42×0.9÷(4.5×2)=0.314(m)$ 答：可以铺 0.314 m 厚。

6. 将一个圆锥从顶点沿高切开，其表面积比原来增加了60 cm²，如果圆锥的高是6 cm，那么圆锥的体积是( )cm³。

答案： 157@@解析：根据题意，把一个圆锥沿高平均分成体积相等、形状相同的两部分，增加了两个截面，每个截面都是高为 6 cm、底等于圆锥的底面直径的三角形，根据三角形的面积计算公式求出三角形的底（圆锥的底面直径），再由圆锥的体积公式列式解答即可。$60÷2×2÷6 = 10(cm)$，$\frac{1}{3}×3.14×(10÷2)^{2}×6 = 157(cm^{3})$。