第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
三、按要求计算。
1. 求下面图形的表面积。
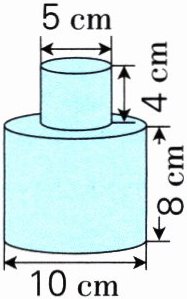
2. 求下面图形的体积。
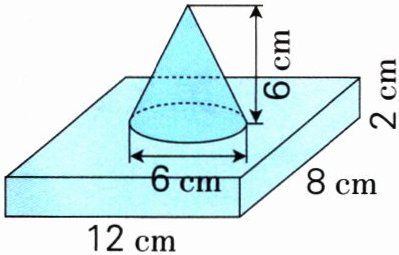
1. 求下面图形的表面积。

2. 求下面图形的体积。

答案:
3.14×(10÷2)²×2 + 3.14×10×8 + 3.14×5×4 = 471(cm²)@@12×8×2 + 1/3×3.14×(6÷2)²×6 = 248.52(cm³)
四、解决问题。
1. 沙漏是我国古代的一种计时工具,又称沙钟。非遗课堂上,小夕制作了一个简易沙漏(如图),上、下两部分都是底面半径是5 cm、高是6 cm的圆锥形,在沙漏上半部分装满沙子。若每分钟向下漏10$cm^{3}$的沙子,则沙子全部漏到下半部分需要多少分钟?(厚度不计)
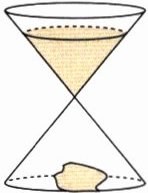
1. 沙漏是我国古代的一种计时工具,又称沙钟。非遗课堂上,小夕制作了一个简易沙漏(如图),上、下两部分都是底面半径是5 cm、高是6 cm的圆锥形,在沙漏上半部分装满沙子。若每分钟向下漏10$cm^{3}$的沙子,则沙子全部漏到下半部分需要多少分钟?(厚度不计)

答案:
1/3×3.14×5²×6 = 157(cm³)
157÷10 = 15.7(分)
答:沙子全部漏到下半部分需要15.7分钟。
解析:由题图可知,沙子的体积等于一个底面半径是5 cm、高是6 cm的圆锥的体积,据此先求出沙子的体积,再除以10即为所求。
2. [新趋势·思维探究]石文化源远流长,小东爸爸有一块形状不规则的观赏石,小东利用两种方法测量这块观赏石的体积。
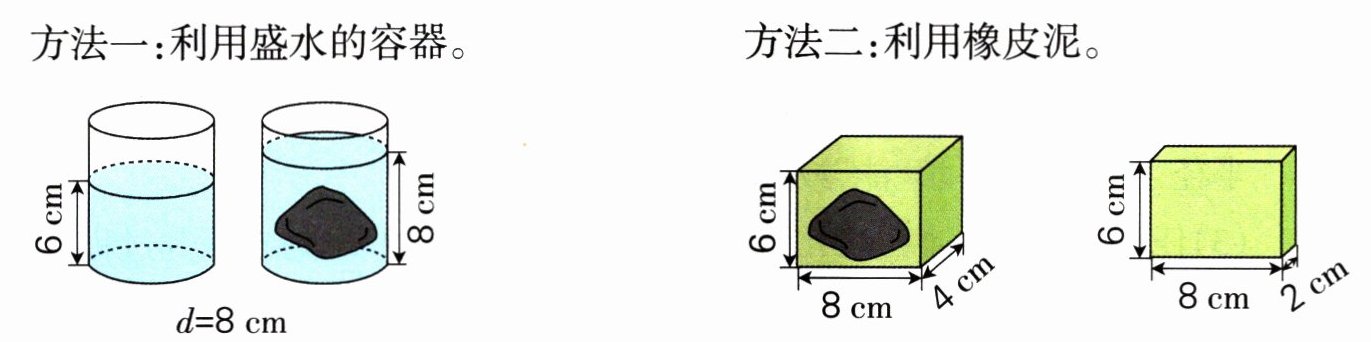
(1)这两种方法相同的地方是:______________________________。
(2)请选择你喜欢的一种方法计算这块观赏石的体积。($\pi$取3)

(1)这两种方法相同的地方是:______________________________。
(2)请选择你喜欢的一种方法计算这块观赏石的体积。($\pi$取3)
答案:
运用了转化思想,把观赏石的体积转化成了规则图形的体积(答案不唯一,合理即可)@@方法一:3×(8÷2)²×(8 - 6) = 96(cm³) 方法二:8×4×6 - 8×2×6 = 96(cm³) 答:这块观赏石的体积是96 cm³。
3. [教材改编]漆扇摇出“国潮”风!漆扇使用了漆艺中的“漂漆”技法。如图,在密闭的容器(高15 cm)中装有一些水和颜料,将这个容器倒过来,这时液面距底部的高度是多少厘米?


答案:
6×1/3 + (10 - 6) = 6(cm) 答:这时液面距底部的高度是6 cm。 解析:液体的体积不变,故相当于圆柱和圆锥的体积变为圆柱的体积,体积和底面积分别相等的圆锥的高是圆柱高的3倍,据此解答即可。
查看更多完整答案,请扫码查看


