2025年智慧学堂九年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂九年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列函数中,属于二次函数的是 ( )
A. $y = 2x - 3$
B. $y=(x + 1)^2 - x^2$
C. $y = 2x(x + 1)$
D. $y=-\frac{2}{x^2}$
A. $y = 2x - 3$
B. $y=(x + 1)^2 - x^2$
C. $y = 2x(x + 1)$
D. $y=-\frac{2}{x^2}$
答案:
C
2. 若函数$y=(m - 2)x^2 + 3x - 1$($m$为常数)是二次函数,则 ( )
A. $m\neq - 2$
B. $m\neq 2$
C. $m\neq 3$
D. $m\neq - 3$
A. $m\neq - 2$
B. $m\neq 2$
C. $m\neq 3$
D. $m\neq - 3$
答案:
B
3. 若$y=(3 - m)x^{m^2 - 7}$是二次函数,则$m$的值为 ( )
A. 3
B. - 3
C. $\pm 3$
D. 0
A. 3
B. - 3
C. $\pm 3$
D. 0
答案:
B
4. 已知两个变量$x$,$y$之间的关系式为$y=(a - 2)x^2+(b + 2)x - 3$.
(1)当_______时,$x$,$y$之间是二次函数关系;
(2)当_______时,$x$,$y$之间是一次函数关系.
(1)当_______时,$x$,$y$之间是二次函数关系;
(2)当_______时,$x$,$y$之间是一次函数关系.
答案:
(1)$a\neq2$;
(2)$a = 2$且$b\neq - 2$
(1)$a\neq2$;
(2)$a = 2$且$b\neq - 2$
5. (重庆一中月考)二次函数$y = x^2 + 2x - 7$的函数值是8,那么对应的$x$的值是 ( )
A. 3
B. 5
C. - 3和5
D. 3和 - 5
A. 3
B. 5
C. - 3和5
D. 3和 - 5
答案:
D
6. (教材$P_{4}T_{3}$变式)已知二次函数$y = x^2 + kx - 8$,当$x = 2$时,$y = - 8$,则当$x = - 1$时,$y =$_______.
答案:
- 5
7. 等边三角形的边长为$a$,面积为$S$,那么$S$与$a$的函数关系式是 ( )
A. $S=\frac{1}{2}a^2$
B. $S=\frac{\sqrt{3}}{2}a^2$
C. $S=\frac{\sqrt{3}}{4}a^2$
D. $S=\frac{\sqrt{2}}{4}a^2$
A. $S=\frac{1}{2}a^2$
B. $S=\frac{\sqrt{3}}{2}a^2$
C. $S=\frac{\sqrt{3}}{4}a^2$
D. $S=\frac{\sqrt{2}}{4}a^2$
答案:
C
8. (新素材·绿色环保)新版《北京市生活垃圾管理条例》实施,以社区为主战场,以家庭分类为基础,正确建立起垃圾分类绿色环保文化,树立社会文明新风尚,为方便市民进行垃圾分类投放,某环保公司第一个月投放$a$个垃圾桶,计划第三个月投放垃圾桶$y$个. 设该公司第二、三个月投放垃圾桶数量的月平均增长率为$x$,那么$y$与$x$之间的函数关系式是 ( )
A. $y=a(1 + x)^2$
B. $y=a(1 - x)^2$
C. $y=a(1 - x)^2+a$
D. $y=x^2+a$
A. $y=a(1 + x)^2$
B. $y=a(1 - x)^2$
C. $y=a(1 - x)^2+a$
D. $y=x^2+a$
答案:
A
9. 菱形的两条对角线之和是26,则菱形的面积$S(cm^2)$与一条对角线的长$x(cm)$之间的函数关系式为__________,自变量$x$的取值范围是__________.
答案:
$S=\frac{1}{2}x\cdot(26 - x)$;$0\lt x\lt26$
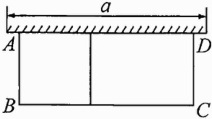
10. 如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度$a$为10米)围成中间隔有一道篱笆的长方形花圃,设花圃的宽$AB$为$x$米,面积为$S$平方米.
(1)求$S$与$x$之间的函数关系式;
(2)如果要围成面积为45平方米的花圃,那么$AB$的长为多少米?
(1)求$S$与$x$之间的函数关系式;
(2)如果要围成面积为45平方米的花圃,那么$AB$的长为多少米?

答案:
解:
(1)$S = x(24 - 3x)$,即$S=-3x^{2}+24x$;
(2)当$S = 45$时,$-3x^{2}+24x = 45$,解得$x_{1}=3$,$x_{2}=5$,又$\because$当$x = 3$时,$BC = 24 - 3x = 15\gt10$(舍去),$\therefore x = 5$,即$AB$的长为 5 米.
(1)$S = x(24 - 3x)$,即$S=-3x^{2}+24x$;
(2)当$S = 45$时,$-3x^{2}+24x = 45$,解得$x_{1}=3$,$x_{2}=5$,又$\because$当$x = 3$时,$BC = 24 - 3x = 15\gt10$(舍去),$\therefore x = 5$,即$AB$的长为 5 米.
查看更多完整答案,请扫码查看


