2025年名校真题卷七年级数学上册沪科版安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校真题卷七年级数学上册沪科版安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
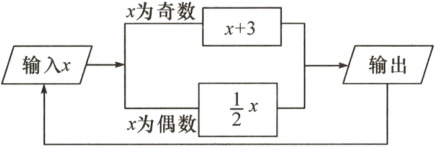
10. 如图,这是一个“数值转换机”,若开始输入x的值是8,则第1次输出的结果是4,第2次输出的结果是2……则第2025次输出的结果是 (
A.8
B.4
C.2
D.1
D
)
A.8
B.4
C.2
D.1
答案:
10. D【答案详解】由题意可知,$\because$开始输入$x$的值是$8$,$\therefore$第$1$次输出的结果是$4$,第$2$次输出的结果是$2$,第$3$次输出的结果是$1$,第$4$次输出的结果是$4·s·s$由此可见,从第$1$次输出的结果开始按$4$,$2$,$1$循环.又$\because 2025÷3 = 675$,$\therefore$第$2025$次输出的结果是$1$.故选:D.
11. 写出一个系数为5,次数为3的单项式:
$5x^{3}$(答案不唯一)
.
答案:
11. $5x^{3}$(答案不唯一) 【答案详解】由题意,这个单项式可以为$5x^{3}$.故答案为:$5x^{3}$(答案不唯一).
12. 若代数式$ mx^{2} + 5y^{2} - 7x^{2} + 3 $的值与字母x的取值无关,则m的值是
7
.
答案:
12. 7 【答案详解】原式$=(m - 7)x^{2} + 5y^{2} + 3.\because$代数式$mx^{2} + 5y^{2} - 2x^{2} + 3$的值与字母$x$的取值无关,$\therefore m - 7 = 0.\therefore m = 7$.故答案为:$7$.
13. 已知a,b,c在数轴上的对应点如图所示,则$ |a + b| - |a - c| - |c - b| = $

$-2a - 2b + 2c$
.
答案:
13. $-2a - 2b + 2c$ 【答案详解】由图可知,$a + b < 0$,$a - c > 0$,$c - b < 0$,$\therefore |a + b| - |a - c| - |c - b| = -(a + b) - (a - c) - (c - b) = -2a - 2b + 2c$.故答案为:$-2a - 2b + 2c$.
14. 对整式A,B定义新运算“#”和“※”: $ A \# B = 3A + 2B $, $ n※A = \underbrace{A \# A \# ·s \# A}_{n个A} $(n是正整数,特别地,$ 1※A = A $),已知$ A = x^{2} + 2xy $.
(1)$ 2※A = $
(2)若$ n※A $的计算结果中xy的系数大于100,则n至少是
(1)$ 2※A = $
$5x^{2} + 10xy$
;(用含x,y的代数式表示)(2)若$ n※A $的计算结果中xy的系数大于100,则n至少是
4
.
答案:
14.
(1)$5x^{2} + 10xy$
(2)4 【答案详解】
(1)$\because A\#B = 3A + 2B$,$n\#A = A\#A·s\#A$($n$是正整数,特别地,$1\#A = A$),$A = x^{2} + 2xy$,$\therefore 2\#A = A\#A = 3A + 2A = 5A = 5(x^{2} + 2xy) = 5x^{2} + 10xy$.故答案为:$5x^{2} + 10xy$.
(2)由
(1)知,$2\#A = A\#A = 5A = 5x^{2} + 10xy$,$\therefore 3\#A = A\#A\#A = 5A\#A = 17A = 17(x^{2} + 2xy) = 17x^{2} + 34xy$,$4\#A = A\#A\#A\#A = 17A\#A = 53A = 53(x^{2} + 2xy) = 53x^{2} + 106xy$.$\because 34 < 100 < 106$,$\therefore n\#A$的计算结果中$xy$的系数大于$100$,$n$至少是$4$.故答案为:$4$.
(1)$5x^{2} + 10xy$
(2)4 【答案详解】
(1)$\because A\#B = 3A + 2B$,$n\#A = A\#A·s\#A$($n$是正整数,特别地,$1\#A = A$),$A = x^{2} + 2xy$,$\therefore 2\#A = A\#A = 3A + 2A = 5A = 5(x^{2} + 2xy) = 5x^{2} + 10xy$.故答案为:$5x^{2} + 10xy$.
(2)由
(1)知,$2\#A = A\#A = 5A = 5x^{2} + 10xy$,$\therefore 3\#A = A\#A\#A = 5A\#A = 17A = 17(x^{2} + 2xy) = 17x^{2} + 34xy$,$4\#A = A\#A\#A\#A = 17A\#A = 53A = 53(x^{2} + 2xy) = 53x^{2} + 106xy$.$\because 34 < 100 < 106$,$\therefore n\#A$的计算结果中$xy$的系数大于$100$,$n$至少是$4$.故答案为:$4$.
15. 计算:$ 3x^{2}y - 4xy^{2} - 3 + 5x^{2}y + 2xy^{2} + 5 $.
答案:
15. 解:原式$= 3x^{2}y + 5x^{2}y - 4xy^{2} + 2xy^{2} - 3 + 5 = (3x^{2}y + 5x^{2}y) + (-4xy^{2} + 2xy^{2}) + (-3 + 5) = (3 + 5)x^{2}y + (-4 + 2)xy^{2} + (-3 + 5) = 8x^{2}y - 2xy^{2} + 2$.
16. 已知多项式$ x^{2}y^{|2 - m|} + xy^{3} - 3x^{4} - 6 $是关于x,y的八次四项式.
(1)求m的值;
(2)把这个多项式按x的降幂重新排列.
(1)求m的值;
(2)把这个多项式按x的降幂重新排列.
答案:
16. 解:
(1)由题意可知,$12 - m + 2 = 8$,$\therefore m = 6$.
(2)这个多项式按$x$的降幂排列为$-3x^{4} + x^{2}y^{6} + xy^{3} - 6$.
(1)由题意可知,$12 - m + 2 = 8$,$\therefore m = 6$.
(2)这个多项式按$x$的降幂排列为$-3x^{4} + x^{2}y^{6} + xy^{3} - 6$.
查看更多完整答案,请扫码查看


