《2025年名校真题卷七年级数学上册沪科版安徽专版》

20. 已知关于$ x,y $的方程组$ \begin{cases} 3x - \frac{5}{2}y = \frac{k}{2} + 3, \\ - \frac{5}{2}x + 3y = - 3k - 1. \end{cases} $
(1)若$ k = 2 $,求这个方程组的解;
(2)若这个方程组的解满足$ x + y = 8 $,求$ k $的值.

答案： 20.解:
(1)当$k = 2$时，这个方程组可化为$\begin{cases}3x - \frac{5}{2}y = 4,① \\ -\frac{5}{2}x + 3y = -7,② \end{cases}$
　　①×12，得$36x - 30y = 48$③，②×10，得$-25x + 30y = -70$④，由③ + ④，得$11x = -22$，解得$x = -2$.将$x = -2$代入②，得$5 + 3y = -7$，解得$y = -4$.$\therefore$当$k = 2$时，这个方程组的解为$\begin{cases}x = -2, \\ y = -4 \end{cases}$
(2)$\begin{cases}3x - \frac{5}{2}y = \frac{k}{2} + 3,① \\ -\frac{5}{2}x + 3y = -3k - 1,② \end{cases}$由① + ②，得$\frac{1}{2}x + \frac{1}{2}y = -\frac{5}{2}k + 2$.$\because x + y = 8$，$\therefore -\frac{5}{2}k + 2 = 4$，解得$k = -\frac{4}{5}$.

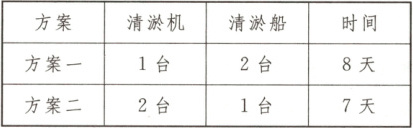
21. 南淝河,古称施水,长江流域巢湖的支流,是合肥的母亲河.为了确保该河道畅通,现需要对一段河道进行清淤处理,清淤任务由两栖反铲式清淤机和小型链斗式清淤船进行.下表是工程队给出的两个工程预备方案,环保部门要求6天内必须完成任务.如果工程部门提供2台清淤机和2台清淤船,共同完成此项任务,那么能否按要求完成任务?

答案： 21.解:设一台清淤机的工作效率为$x$，一台清淤船的工作效率为$y$.根据题意，得$\begin{cases}x + 2y = \frac{1}{8}, \\ 2x + y = \frac{1}{7} \end{cases}$解得$\begin{cases}x = \frac{3}{56}, \\ y = \frac{1}{28} \end{cases}$$\therefore 6×(2×\frac{3}{56} + 2×\frac{1}{28})=\frac{15}{14} ＞ 1$.答:2台清淤机和2台清淤船共同工作，能按要求完成任务.