《2025年名校真题卷七年级数学上册沪科版安徽专版》

20. 仔细观察下列等式：
第 1 个：$5^{2}-1^{2}=8×3$；
第 2 个：$9^{2}-5^{2}=8×7$；
第 3 个：$13^{2}-9^{2}=8×11$；
第 4 个：$17^{2}-13^{2}=8×15$；
……
(1)请写出第 6 个等式：_；

(2)请写出第 n 个等式：_(用含字母 n 的等式表示)；
(3)运用上述规律，计算：$8×11 + 8×15 + ·s + 8×95 + 8×99$。

答案： 20.解：$(1)25^{2}-21^{2}=8×23$
$(2)(4n+1)^{2}-(4n-3)^{2}=8(4n-1).【$答案详解】
(1)由题意可得，第6个等式：$25^{2}-21^{2}=8×23.$故答案为：$25^{2}-21^{2}=8×23.(2)$由题意可得，第n个等式：$(4n+1)^{2}-(4n-3)^{2}=8(4n-1).$故答案为：$(4n+1)^{2}-(4n-3)^{2}=8(4n-1).$
(3)原式$=(13^{2}-9^{2})+(17^{2}-13^{2})+·s+(97^{2}-93^{2})+(101^{2}-97^{2})=13^{2}-9^{2}+17^{2}-13^{2}+·s+97^{2}-93^{2}+101^{2}-97^{2}=101^{2}-9^{2}=10201-81=10120.$

21. 某超市进行商品促销活动，一次性买够一定质量的猪肉就会有优惠，原价为 50 元/千克的猪肉按照如下活动进行售卖：

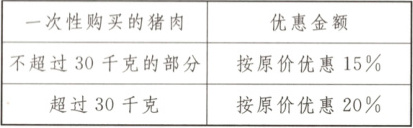
（1）某餐馆打算一次性购买猪肉 45 千克，若在促销期间购买，则该餐馆会比按原价购买节省多少钱？
（2）若某顾客打算一次性购买猪肉 a 千克，请用含 a 的代数式表示促销期间这个顾客的花费；
（3）促销期间，某校食堂准备购买 80 千克猪肉，采购员计划了两种购买方案：
方案一：一次性购买猪肉 80 千克；
方案二：分两次购买，每次购买猪肉 40 千克；计算说明哪种方案更划算？并求出两种方案相差的金额。

答案： 21.解：
(1)由条件可知，节省金额为30×50×15%+(45-30)×50×20%=375(元).
(2)当0≤a≤30时，花费为a×50×(1-15%)=42.5a(元)；当a＞30时，花费为30×50×(1-15%)+(a-30)×50×(1-20%)=(40a+75)元.
(3)方案一花费：40×80+75=3275(元)；方案二花费：2×(40×40+75)=3350(元)，$\because 3275＜3350,\therefore $方案一划算，相差的金额为3350-3275=75(元).