2025年名校真题卷七年级数学上册沪科版安徽专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校真题卷七年级数学上册沪科版安徽专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 已知岛$P$位于岛$Q$的正西方,从岛$P$,$Q$分别测得船$R$位于南偏东$30°$和南偏西$45°$方向上,则符合条件的示意图是 (

D
)
答案:
8.D[答案详解]因为从岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,
∴D选项符合题意.故选:D.
∴D选项符合题意.故选:D.
9. 如图,$O$为直线$AB$上一点,$OC$平分$\angle AOD$,$\angle BOD = 4\angle DOE$.若$\angle COE = 70°$,则$\angle DOE$的度数为 (
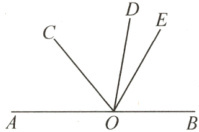
A.$20°$
B.$18°$
C.$22°$
D.$15°$
A
)
A.$20°$
B.$18°$
C.$22°$
D.$15°$
答案:
9.A [答案详解]由题意可知,OC平分∠AOD,
∴2∠COD = ∠AOD.
∵∠COE = 70°,
∴∠COD = ∠COE - ∠DOE = 70° - ∠DOE.
∵∠AOD + ∠BOD = 180°,∠BOD = 4∠DOE,
∴2(70° - ∠DOE) + 4∠DOE = 180°,解得∠DOE = 20°.故选:A.
∴2∠COD = ∠AOD.
∵∠COE = 70°,
∴∠COD = ∠COE - ∠DOE = 70° - ∠DOE.
∵∠AOD + ∠BOD = 180°,∠BOD = 4∠DOE,
∴2(70° - ∠DOE) + 4∠DOE = 180°,解得∠DOE = 20°.故选:A.
10. 如图,点$M$在线段$AN$的延长线上,且线段$MN = 10$,第一次操作:分别取线段$AM$和$AN$的中点$M_1$,$N_1$;第二次操作:分别取线段$AM_1$和$AN_1$的中点$M_2$,$N_2$;第三次操作:分别取线段$AM_2$和$AN_2$的中点$M_3$,$N_3·s·s$连续这样操作$20$次,则$M_{20}N_{20} =$ (

A.$\frac{5}{2^{18}}$
B.$\frac{5}{2^{19}}$
C.$\frac{5}{2^{20}}$
D.$\frac{5}{2^{21}}$
B
)
A.$\frac{5}{2^{18}}$
B.$\frac{5}{2^{19}}$
C.$\frac{5}{2^{20}}$
D.$\frac{5}{2^{21}}$
答案:
10.B [答案详解]由条件可知,$M_1N_1$ = AM₁ - AN₁ = $\frac{1}{2}$AM - $\frac{1}{2}$AN = $\frac{1}{2}$(AM - AN) = $\frac{1}{2}$MN = $\frac{1}{2}$×10 = $\frac{10}{2}$.
∵M₂,N₂分别为AM₁,AN₁的中点,
∴M₂N₂ = AM₂ - AN₂ = $\frac{1}{2}$AM₁ - $\frac{1}{2}$AN₁ = $\frac{1}{2}$(AM₁ - AN₁) = $\frac{1}{2}$MN = $\frac{1}{2}$×$\frac{10}{2}$ = $\frac{10}{{2}^2}$.
∵M₃,N₃分别为AM₂,AN₂的中点,
∴M₃N₃ = AM₃ - AN₃ = $\frac{1}{2}$AM₂ - $\frac{1}{2}$AN₂ = $\frac{1}{2}$(AM₂ - AN₂) = $\frac{1}{2}$M₂N₂ = $\frac{1}{2}$×$\frac{10}{{2}^2}$ = $\frac{10}{{2}^3}$.根据规律得到$M_nN_n$ = $\frac{10}{{2}^n}$,
∴$M_{20}N_{20}$ = $\frac{10}{{2}^{20}}$ = $\frac{5}{{2}^{19}}$.故选:B.
∵M₂,N₂分别为AM₁,AN₁的中点,
∴M₂N₂ = AM₂ - AN₂ = $\frac{1}{2}$AM₁ - $\frac{1}{2}$AN₁ = $\frac{1}{2}$(AM₁ - AN₁) = $\frac{1}{2}$MN = $\frac{1}{2}$×$\frac{10}{2}$ = $\frac{10}{{2}^2}$.
∵M₃,N₃分别为AM₂,AN₂的中点,
∴M₃N₃ = AM₃ - AN₃ = $\frac{1}{2}$AM₂ - $\frac{1}{2}$AN₂ = $\frac{1}{2}$(AM₂ - AN₂) = $\frac{1}{2}$M₂N₂ = $\frac{1}{2}$×$\frac{10}{{2}^2}$ = $\frac{10}{{2}^3}$.根据规律得到$M_nN_n$ = $\frac{10}{{2}^n}$,
∴$M_{20}N_{20}$ = $\frac{10}{{2}^{20}}$ = $\frac{5}{{2}^{19}}$.故选:B.
11. 一个角的度数为$28°$,那么这个角的补角的度数为
152°
.
答案:
11.152° [答案详解]
∵一个角的度数为28°,
∴这个角的补角的度数是180° - 28° = 152°.故答案为:152°.
∵一个角的度数为28°,
∴这个角的补角的度数是180° - 28° = 152°.故答案为:152°.
12. 如图,点$B$在线段$AC$上,此时图中共有$m$条线段,若在线段$BC$上增加一点$D$(点$D$不与点$B$,$C$重合),此时图中共有$n$条线段,则$n - m =$

3
.
答案:
12.3 [答案详解]增加点D后增加了AD,BD,CD共3条线段,所以n - m = 3.故答案为:3.
13. 如图,点$C$,$D$,$E$在线段$AB$上,且$AC : CD = 2 : 3$,$E$为$CB$的中点.若$DE = 3$,$AB = 30$,则$AE$的长为
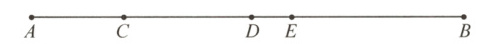
18
.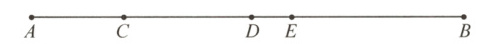
答案:
13.18 [答案详解]设AC = 2x,则CD = 3x,CE = 3x + 3.
∵E 为CB的中点,
∴BE = CE = 3x + 3.
∵AB = AC + CE + BE = 30,
∴2x + (3x + 3) + (3x + 3) = 30,解得x = 3.
∴AC = 2×3 = 6,CE = 3×3 + 3 = 12.
∴AE = AC + CE = 6 + 12 = 18.故答案为:18.
∵E 为CB的中点,
∴BE = CE = 3x + 3.
∵AB = AC + CE + BE = 30,
∴2x + (3x + 3) + (3x + 3) = 30,解得x = 3.
∴AC = 2×3 = 6,CE = 3×3 + 3 = 12.
∴AE = AC + CE = 6 + 12 = 18.故答案为:18.
14. 定义:如果一个角内部的一条射线将这个角分成两个角,其中一个角是另一个角的$n$倍,那么我们将这条射线称为这个角的$n + 1$分位线.例如:如图1,$\angle MOP = 4\angle NOP$,则$OP$为$\angle MON$的$5$分位线;$\angle NOQ = 4\angle MOQ$,则$OQ$也是$\angle MON$的$5$分位线.
(1) 如图2,点$A$,$O$,$B$在同一条直线上,$OC$为一条射线,$OP$,$OQ$分别为$\angle AOC$与$\angle BOC$的$3$分位线,($\angle COP>\angle POA$,$\angle COQ>\angle QOB$),$\angle AOC = 150°$,则$\angle POQ =$
(2) 若点$A$,$O$,$B$在同一条直线上,$OC$为一条射线,已知射线$OM$,$ON$分别为$\angle AOC$与$\angle BOC$的$5$分位线,且$\angle MON = 96°$,则$\angle AOC =$
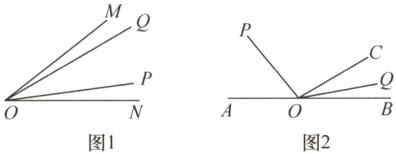
(1) 如图2,点$A$,$O$,$B$在同一条直线上,$OC$为一条射线,$OP$,$OQ$分别为$\angle AOC$与$\angle BOC$的$3$分位线,($\angle COP>\angle POA$,$\angle COQ>\angle QOB$),$\angle AOC = 150°$,则$\angle POQ =$
120°
;(2) 若点$A$,$O$,$B$在同一条直线上,$OC$为一条射线,已知射线$OM$,$ON$分别为$\angle AOC$与$\angle BOC$的$5$分位线,且$\angle MON = 96°$,则$\angle AOC =$
80°或100°
.
答案:
14.
(1)120° [答案详解]
∵OP,OQ分别为∠AOC与∠BOC 的3分位线,∠COP>∠POA,∠COQ>∠QOB,
∴∠POC = 2∠AOP,∠COQ = 2∠BOQ.
∵∠AOC = 150°,点A,O,B在同一条直线上,
∴∠AOP = $\frac{1}{3}$∠AOC = 50°,∠BOQ = $\frac{1}{3}$∠BOC = 10°.
∴∠POC = 100°,∠COQ = 20°.
∴∠POQ = 100° + 20° = 120°.故答案为:120°.
(2)80°或100° [答案详解]根据题意,分四种情况讨论:①若∠MOC = 4∠MOA,∠NOC = 4∠BON,则∠MOC + ∠NOC = ∠MON = 96°,∠MOA + ∠BON = 96°÷4 = 24°.又
∵∠MOA + ∠BON = 180° - ∠MON = 84°,两者相矛盾,舍去;②如图3,若∠MOA = 4∠MOC,∠NOC = 4∠BON,设∠MOC = x,∠BON = y.根据题意,得$\begin{cases}x + 4y = 96°\\4x + y = 84°\end{cases}$解得$\begin{cases}x = 16°\\y = 20°\end{cases}$
∴∠AOC = 5x = 80°;

③如图4,若∠MOC = 4∠MOA,∠NOB = 4∠CON,同理可得,∠AOC = 100°;

④若∠MOA = 4∠MOC,∠BON = 4∠NOC,不符合题意,舍去.
综上所述,∠AOC的度数为80°或100°.故答案为:80°或100°.
14.
(1)120° [答案详解]
∵OP,OQ分别为∠AOC与∠BOC 的3分位线,∠COP>∠POA,∠COQ>∠QOB,
∴∠POC = 2∠AOP,∠COQ = 2∠BOQ.
∵∠AOC = 150°,点A,O,B在同一条直线上,
∴∠AOP = $\frac{1}{3}$∠AOC = 50°,∠BOQ = $\frac{1}{3}$∠BOC = 10°.
∴∠POC = 100°,∠COQ = 20°.
∴∠POQ = 100° + 20° = 120°.故答案为:120°.
(2)80°或100° [答案详解]根据题意,分四种情况讨论:①若∠MOC = 4∠MOA,∠NOC = 4∠BON,则∠MOC + ∠NOC = ∠MON = 96°,∠MOA + ∠BON = 96°÷4 = 24°.又
∵∠MOA + ∠BON = 180° - ∠MON = 84°,两者相矛盾,舍去;②如图3,若∠MOA = 4∠MOC,∠NOC = 4∠BON,设∠MOC = x,∠BON = y.根据题意,得$\begin{cases}x + 4y = 96°\\4x + y = 84°\end{cases}$解得$\begin{cases}x = 16°\\y = 20°\end{cases}$
∴∠AOC = 5x = 80°;

③如图4,若∠MOC = 4∠MOA,∠NOB = 4∠CON,同理可得,∠AOC = 100°;

④若∠MOA = 4∠MOC,∠BON = 4∠NOC,不符合题意,舍去.
综上所述,∠AOC的度数为80°或100°.故答案为:80°或100°.
查看更多完整答案,请扫码查看


