第95页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1. 儿童乐园中,有两块相似三角形的场地,且相似比为 $2:3$,面积的差为 $30m^{2}$。有下列结论:① 这两块地的周长比为 $2:3$;② 这两块地的面积比为 $2:3$;③ 这两块地的面积之和为 $78m^{2}$;④ 这两块地的对应高的比为 $2:3$。其中,正确的有(
A.$4$ 个
B.$3$ 个
C.$2$ 个
D.$1$ 个
B
)A.$4$ 个
B.$3$ 个
C.$2$ 个
D.$1$ 个
答案:
1.B
2. (2023·太原杏花岭期中)如图所示为著名画家达·芬奇的名画《蒙娜丽莎》。画中的脸部被包在矩形 $ABCD$ 内,$E$ 是 $AB$ 的黄金分割点,$EF// BC$,交 $DC$ 于点 $F$,$BE>AE$。若 $AB = 2a$,则 $BE$ 的长为(

A.$(\sqrt{5}+1)a$
B.$(\sqrt{5}-1)a$
C.$(3-\sqrt{5})a$
D.$(\sqrt{5}-2)a$
B
)
A.$(\sqrt{5}+1)a$
B.$(\sqrt{5}-1)a$
C.$(3-\sqrt{5})a$
D.$(\sqrt{5}-2)a$
答案:
2.B
3. 如图,一块材料 $ABC$ 的形状是等腰三角形,底边 $BC = 120$,高 $AD = 120$。若把这块材料加工成正方体零件(涂色部分为正方体零件的表面展开图),则正方体零件的棱长为(
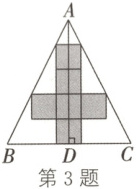
A.$20$
B.$24$
C.$28$
D.$32$
B
)
A.$20$
B.$24$
C.$28$
D.$32$
答案:
3.B
4. (2023·东营)如图,$\triangle ABC$ 为等边三角形,点 $D$,$E$ 分别在边 $BC$,$AB$ 上,$\angle ADE = 60^{\circ}$。若 $BD = 4DC$,$DE = 2.4$,则 $AD$ 的长为(
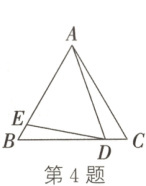
A.$1.8$
B.$2.4$
C.$3$
D.$3.2$
C
)
A.$1.8$
B.$2.4$
C.$3$
D.$3.2$
答案:
4.C 解析:先证∠CAD=∠BDE,再根据∠B=∠C=60°,得出△ADC∽△DEB,
∴$\frac{AD}{DE}=\frac{AC}{DB}$。又
∵BD=4DC,
∴设DC=x,则BD=4x,BC=AC=5x,可得$\frac{AD}{2.4}=\frac{5x}{4x}$,解得AD=3。
∴$\frac{AD}{DE}=\frac{AC}{DB}$。又
∵BD=4DC,
∴设DC=x,则BD=4x,BC=AC=5x,可得$\frac{AD}{2.4}=\frac{5x}{4x}$,解得AD=3。
5. 如图,$D$ 是 $\triangle ABC$ 内一点,点 $E$ 在线段 $BD$ 的延长线上,$BE$ 与 $AC$ 交于点 $O$,连接 $AD$,$CE$。如果 $\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}$,那么下列结论中,正确的是(
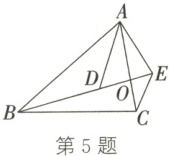
A.$CE// AD$
B.$BD = AD$
C.$\angle ABE = \angle CBE$
D.$BO· AE = AO· BC$
D
)
A.$CE// AD$
B.$BD = AD$
C.$\angle ABE = \angle CBE$
D.$BO· AE = AO· BC$
答案:
5.D
6. 如图,$E$ 是四边形 $ABCD$ 的对角线 $BD$ 上一点,且 $\angle BAC = \angle BDC = \angle DAE$。从图中找出 $1$ 对相似三角形:
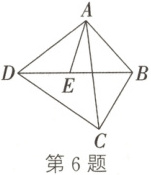
△AEB∽△ADC
。
答案:
6.答案不唯一,如△AEB∽△ADC
7. 如图,在矩形 $ABCD$ 中,$AB = 4$,$BC = 5$,$E$ 为边 $BC$ 延长线上一点,且 $CE = 3$。连接 $AE$ 交边 $CD$ 于点 $F$,过点 $D$ 作 $DH\perp AE$ 于点 $H$,则 $DH =$

$\sqrt{5}$
。
答案:
7.$\sqrt{5}$
8. (2023·潍坊)在《数书九章》中记载了一个测量塔高的问题:如图,$AB$ 的长表示塔的高度,$CD$ 的长表示竹竿顶端到地面的高度,$EF$ 的长表示人眼到地面的高度,$AB$,$CD$,$EF$ 在同一平面内,点 $A$,$C$,$E$ 在同一条水平直线上。已知 $AC = 20$ 米,$CE = 10$ 米,$CD = 7$ 米,$EF = 1.4$ 米,人从点 $F$ 远眺塔顶 $B$,视线恰好经过竹竿的顶端 $D$,可求出塔的高度。根据以上信息,塔的高度为

18.2
米。
答案:
8.18.2
9. 如图,$P$ 为 $□ ABCD$ 的边 $BC$ 上一点,$E$,$F$ 分别为线段 $PA$,$PD$ 上的点,且 $PA = 3PE$,$PD = 3PF$,$\triangle PEF$,$\triangle PDC$,$\triangle PAB$ 的面积分别记为 $S$,$S_{1}$,$S_{2}$。若 $S = 2$,则 $S_{1}+S_{2}=$
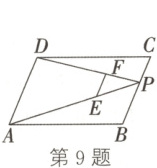
18
。
答案:
9.18
查看更多完整答案,请扫码查看


