第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1. (2022·晋中期中)如图,∠1=∠2,那么添加下列条件后,仍不能判定△ABC与△ADE相似的是(
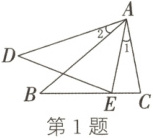
A.∠C=∠AED
B.∠B=∠D
C.$\frac{AB}{AD}=\frac{BC}{DE}$
D.$\frac{AB}{AD}=\frac{AC}{AE}$
C
)
A.∠C=∠AED
B.∠B=∠D
C.$\frac{AB}{AD}=\frac{BC}{DE}$
D.$\frac{AB}{AD}=\frac{AC}{AE}$
答案:
1.C
2. 如图,小明在作业纸上画出①②两组三角形,每组各有两个三角形,其边长和角的度数已在图上标注,对于图①②中的两个三角形,下列说法中,正确的是(
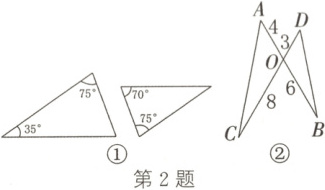
A.都相似
B.都不相似
C.只有①相似
D.只有②相似
A
)
A.都相似
B.都不相似
C.只有①相似
D.只有②相似
答案:
2.A
3. 如图,在等边三角形ABC中,点D,E分别在AC,AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE=BE,连接BD,DE,则下列三角形中,与△AED相似的是(
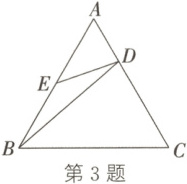
A.△BED
B.△ABD
C.△CBD
D.△ABC
C
)
A.△BED
B.△ABD
C.△CBD
D.△ABC
答案:
3.C
4. (教材P92随堂练习变式)在如图所示的三角形中,
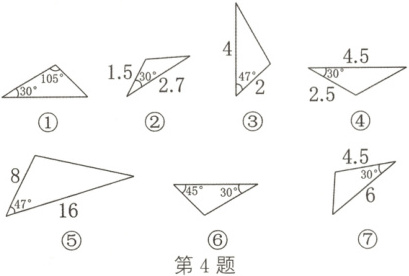
①⑥
相似,②④
相似,③⑤
相似(填序号)。
答案:
4.①⑥ ②④ ③⑤
5. 如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2,连接CD.
(1)△BCD与△BAC相似吗?请说明理由.
(2)若CD=$\frac{5}{3}$,求AC的长.
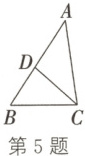
(1)△BCD与△BAC相似吗?请说明理由.
(2)若CD=$\frac{5}{3}$,求AC的长.
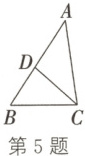
答案:
5.
(1)△BCD∽△BAC 理由:
∵$BD = \frac{4}{3}$,$AB = 3$,$BC = 2$,
∴$\frac{BD}{BC} = \frac{4}{3} ÷ 2 = \frac{2}{3}$,$\frac{BC}{BA} = 2 ÷ 3 = \frac{2}{3}$
∴$\frac{BD}{BC} = \frac{BC}{BA}$
∵∠DBC = ∠CBA,
∴△BCD∽△BAC.
(2)
∵△BCD∽△BAC,
∴$\frac{CD}{AC} = \frac{BC}{BA}$
∵$CD = \frac{5}{3}$,
∴$AC = \frac{5}{2}$
(1)△BCD∽△BAC 理由:
∵$BD = \frac{4}{3}$,$AB = 3$,$BC = 2$,
∴$\frac{BD}{BC} = \frac{4}{3} ÷ 2 = \frac{2}{3}$,$\frac{BC}{BA} = 2 ÷ 3 = \frac{2}{3}$
∴$\frac{BD}{BC} = \frac{BC}{BA}$
∵∠DBC = ∠CBA,
∴△BCD∽△BAC.
(2)
∵△BCD∽△BAC,
∴$\frac{CD}{AC} = \frac{BC}{BA}$
∵$CD = \frac{5}{3}$,
∴$AC = \frac{5}{2}$
6. 如图,BD,CE是△ABC的两条高,它们相交于点F,连接DE.
(1)求证:△ADE∽△ABC.
(2)有下列结论:① △ABD∽△ACE;② △EBF∽△DCF;③ △BEC∽△CDB;④ △DEF∽△CBF.其中,正确的是
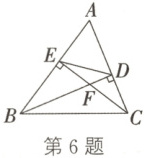
(1)求证:△ADE∽△ABC.
(2)有下列结论:① △ABD∽△ACE;② △EBF∽△DCF;③ △BEC∽△CDB;④ △DEF∽△CBF.其中,正确的是
①②④
(填序号).
答案:
6.
(1)
∵BD,CE是△ABC的高,
∴∠ADB = ∠AEC = 90°.
∵∠A = ∠A,
∴△ABD∽△ACE.
∴$\frac{AB}{AC} = \frac{AD}{AE}$
∴$\frac{AE}{AC} = \frac{AD}{AB}$
∵∠A = ∠A,
∴△ADE∽△ABC
(2)①②④ 解析:
∵∠AEC = ∠ADB = 90°,∠A = ∠A,
∴△ABD∽△ACE.
∵∠BEF = ∠CDF = 90°,∠BFE =
∠CFD,
∴△EBF∽△DCF.在△BEC与△CDB中只有
∠BEC = ∠CDB = 90°,故不能判定△BEC∽△CDB.
∵△EBF∽△DCF,
∴$\frac{EF}{DF} = \frac{BF}{CF}$
∴$\frac{EF}{BF} = \frac{DF}{CF}$
∵∠DFE =
∠CFB,
∴△DEF∽△CBF.综上所述,正确的是①②④.
(1)
∵BD,CE是△ABC的高,
∴∠ADB = ∠AEC = 90°.
∵∠A = ∠A,
∴△ABD∽△ACE.
∴$\frac{AB}{AC} = \frac{AD}{AE}$
∴$\frac{AE}{AC} = \frac{AD}{AB}$
∵∠A = ∠A,
∴△ADE∽△ABC
(2)①②④ 解析:
∵∠AEC = ∠ADB = 90°,∠A = ∠A,
∴△ABD∽△ACE.
∵∠BEF = ∠CDF = 90°,∠BFE =
∠CFD,
∴△EBF∽△DCF.在△BEC与△CDB中只有
∠BEC = ∠CDB = 90°,故不能判定△BEC∽△CDB.
∵△EBF∽△DCF,
∴$\frac{EF}{DF} = \frac{BF}{CF}$
∴$\frac{EF}{BF} = \frac{DF}{CF}$
∵∠DFE =
∠CFB,
∴△DEF∽△CBF.综上所述,正确的是①②④.
查看更多完整答案,请扫码查看


