《2025年通成学典课时作业本九年级数学上册北师大版山西专版》

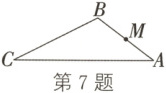
7. 如图，在$\triangle ABC$中，$AB = 2\sqrt{5}$，$AC = 4\sqrt{5}$，$BC = 6$。$M$为$AB$的中点，在线段$AC$上取一点$N$，使$\triangle AMN$与$\triangle ABC$相似，则线段$MN$的长为3或$\frac{3}{2}$。

答案： 7.3或$\frac{3}{2}$

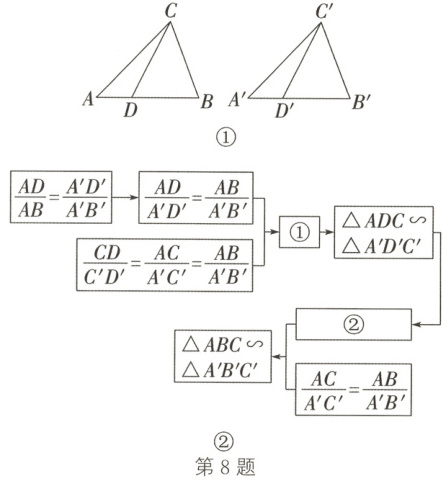
8. 如图①，在$\triangle ABC$和$\triangle A'B'C'$中，$D$，$D'$分别是$AB$，$A'B'$上的点，$\frac{AD}{AB} = \frac{A'D'}{A'B'}$。
(1)填空：当$\frac{CD}{C'D'} = \frac{AC}{A'C'} = \frac{AB}{A'B'}$时，求证$\triangle ABC \sim \triangle A'B'C'$。证明途径如图②所示，其中，空格①：$\frac{CD}{C'D'}$=$\frac{AC}{A'C'}$=$\frac{AD}{A'D'}$，空格②：∠A=∠A'。
(2)当$\frac{CD}{C'D'} = \frac{AB}{A'B'} = \frac{BC}{B'C'}$时，判断$\triangle ABC$与$\triangle A'B'C'$是否相似，并说明理由。

答案： 8.
(1)①$\frac{CD}{C'D'}$=$\frac{AC}{A'C'}$=$\frac{AD}{A'D'}$　②∠A=∠A'　
(2)△ABC与△A'B'C'相似　理由：
∵$\frac{AD}{AB}$=$\frac{A'D'}{A'B'}$，
∴$\frac{AB−AD}{AB}$=$\frac{A'B'−A'D'}{A'B'}$，即$\frac{BD}{AB}$=$\frac{B'D'}{A'B'}$，
∴$\frac{BD}{B'D'}$=$\frac{AB}{A'B'}$.
∵$\frac{CD}{C'D'}$=$\frac{AB}{A'B'}$=$\frac{BC}{B'C'}$，
∴$\frac{CD}{C'D'}$=$\frac{BD}{B'D'}$=$\frac{BC}{B'C'}$.
∴△BDC∽△B'D'C'.
∴∠DBC=∠D'B'C'，
∴△ABC∽△A'B'C'.

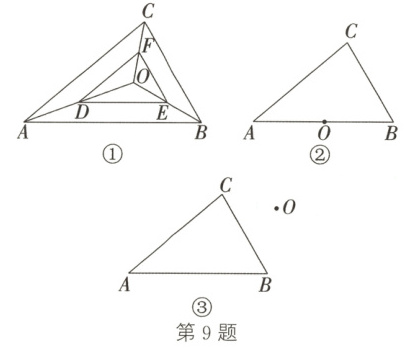
9. 已知$\triangle ABC$与点$O$，连接$OA$，$OB$，$OC$，分别取$OA$，$OB$，$OC$的中点$D$，$E$，$F$，连接$DE$，$EF$，$FD$。
（1）如图①，点$O$在$\triangle ABC$的内部，求证：$\triangle DEF \sim \triangle ABC$；
（2）如图②，点$O$在边$AB$上，请按叙述画图，并直接写出（1）中的结论是否仍成立；
（3）如果点$O$在$\triangle ABC$的外部，请在图③中按叙述画图，并直接写出（1）中的结论是否仍成立。

答案：
9.
(1)
∵D，E，F分别为OA，OB，OC的中点，
∴DE，DF，EF分别是△AOB，△AOC，△BOC的中位线.
∴DE=$\frac{1}{2}$AB，DF=$\frac{1}{2}$AC，EF=$\frac{1}{2}$BC.
∴$\frac{DE}{AB}$=$\frac{DF}{AC}$=$\frac{EF}{BC}$=$\frac{1}{2}$，
∴△DEF∽△ABC　
(2)如图①所示　
(1)中的结论仍成立
(3)如图②所示　
(1)中的结论仍成立