《2025年通成学典课时作业本九年级数学上册北师大版山西专版》

10. (2023·河北)如图，在 $Rt\triangle ABC$ 中，$AB = 4$，$M$ 是斜边 $BC$ 的中点，以 $AM$ 为边作正方形 $AMEF$。若 $S_{正方形AMEF} = 16$，则 $S_{\triangle ABC}$ 的值为(B)

A.$4\sqrt{3}$
B.$8\sqrt{3}$
C.$12$
D.$16$

答案： 10. B

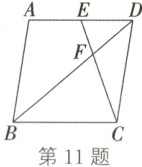
11. (2022·淄博)如图，在边长为 $4$ 的菱形 $ABCD$ 中，$E$ 为边 $AD$ 的中点，连接 $CE$ 交对角线 $BD$ 于点 $F$。若 $\angle DEF = \angle DFE$，则菱形 $ABCD$ 的面积为(B)

A.$16$
B.$6\sqrt{7}$
C.$12\sqrt{7}$
D.$30$

答案： 11. B

12. (2022·恩施)如图，在矩形 $ABCD$ 中，连接 $BD$，分别以点 $B$，$D$ 为圆心，大于 $\dfrac{1}{2}BD$ 的长为半径画弧，两弧交于 $P$，$Q$ 两点，作直线 $PQ$，分别与 $AD$，$BC$ 交于点 $M$，$N$，连接 $BM$，$DN$。若 $AD = 4$，$AB = 2$，则四边形 $MBND$ 的周长为(C)

A.$\dfrac{5}{2}$
B.$5$
C.$10$
D.$20$

答案： 12. C

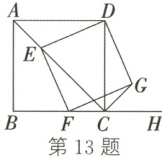
13. 如图，正方形 $ABCD$ 的边长为 $9$，$H$ 为 $BC$ 延长线上一点，$E$ 为对角线 $AC$ 上一点，连接 $DE$，过点 $E$ 作 $EF \perp DE$，交射线 $BC$ 于点 $F$，以 $DE$，$EF$ 为邻边作矩形 $DEFG$，连接 $CG$。下列结论中，不正确的是(B)

A.矩形 $DEFG$ 是正方形
B.$\angle CEF = \angle ADE$
C.$CG$ 平分 $\angle DCH$
D.$CE + CG = 9\sqrt{2}$

答案：
13. B 解析：如图，过点 E 作 EK⊥BC 于点 K，EL⊥CD 于点 L，证明四边形 ELCK 是正方形，则 EK = EL. 证明△FEK≌△DEL，得 DE = FE，即可证明矩形 DEFG 是正方形，故选项 A 正确. 由∠CDG = ∠ADE = 90° - ∠CDE，CD = AD，GD = ED，证明△CDG≌△ADE，得 CG = AE，则 CE + CG = AC 为定值，再根据勾股定理求出 AC 的长为 9$\sqrt{2}$，故选项 D 正确. 由△CDG≌△ADE，得 ∠DCG = ∠DAE = 45°，易得 ∠DCG = ∠GCH = 45°，故选项 C 正确. 根据 ∠ADE = ∠DEL = ∠FEK ≠ ∠CEF，可以判断选项 B 不正确.

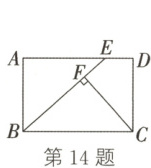
14. (2023·台州)如图，在矩形 $ABCD$ 中，$AB = 4$，$AD = 6$。在边 $AD$ 上取一点 $E$，使 $BE = BC$，过点 $C$ 作 $CF \perp BE$，垂足为 $F$，则 $BF$ 的长为 2$\sqrt{5}$。

答案： 14. 2$\sqrt{5}$

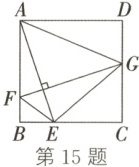
15. (2023·太原小店期中)如图，在正方形 $ABCD$ 中，$AB = 3$，$E$ 是边 $BC$ 上一点，且 $CE = 2BE$，连接 $AE$，$F$ 是边 $AB$ 上一点，过点 $F$ 作 $FG \perp AE$ 交 $CD$ 于点 $G$，连接 $EF$，$EG$，$AG$，则四边形 $AFEG$ 的面积为 5。

答案： 15. 5

16. (2023·运城稷山期中)如图，在菱形 $ABCD$ 中，$AB = 10$，$BD = 16$，若 $M$，$N$ 分别是边 $AD$，$BC$ 上的动点，且 $AM = BN$，作 $ME \perp BD$，$NF \perp BD$，垂足分别为 $E$，$F$，则 $ME + NF$ 的值为 6。

答案：
16. 6 解析：如图，连接 AC 交 BD 于点 O，过点 M 作 MG//BD 交 AC 于点 G，则可得四边形 MEOG 是矩形. 证明△NFB≌△AGM，从而得 NF = AG. 由 ME = OG，得 ME + NF = OG + AG = AO. 运用勾股定理求出 AO 的长即可.

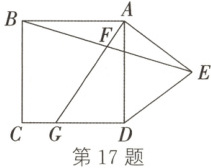
17. (2023·天津)如图，在边长为 $3$ 的正方形 $ABCD$ 的外侧，作等腰三角形 $ADE$，$EA = ED = \dfrac{5}{2}$。
(1)$\triangle ADE$ 的面积为 3；
(2)若 $F$ 为 $BE$ 的中点，连接 $AF$ 并延长，与 $CD$ 相交于点 $G$，则 $AG$ 的长为 $\sqrt{13}$。

答案： 17.
(1) 3 解析：过点 E 作 EM⊥AD 于点 M. 根据等腰三角形的性质，得到 AM = DM = $\frac{1}{2}$AD = $\frac{3}{2}$，根据勾股定理，得到 EM = $\sqrt{AE^2 - AM^2}$ = 2，根据三角形的面积公式即可得到△ADE 的面积为 $\frac{1}{2}$AD · EM = $\frac{1}{2}$×3×2 = 3.
(2) $\sqrt{13}$ 解析：过点 E 作 AD 的垂线分别与 AD，AG，BC 交于点 M，N，P. 根据正方形的性质，得到 EP⊥BC，推出四边形 ABPM 是矩形，得到 PM = AB = 3，AB//EP. 证△ABF≌△NEF，得 EN = BA = 3. 由
(1)，易得 MN = 1. 证明三角形的中位线，得 GD = 2. 根据勾股定理，可求 AG = $\sqrt{AD^2 + GD^2}$ = $\sqrt{13}$.

18. （2023·运城池湖期中）如图，在四边形 $ABCD$ 中，$\angle ABC = 90^{\circ}$，$AD // BC$，$AD = BC$，$E$ 是 $AD$ 上一点，连接 $BE$，$CE$，且 $\angle BEC = 90^{\circ}$，$F$ 是 $BC$ 的中点，连接 $EF$。
（1）求证：四边形 $ABCD$ 是矩形；
（2）若 $\angle ECD = 30^{\circ}$，$EF = 4$，求四边形 $ABCD$ 的面积。

答案：
(1)
∵ AD//BC，AD = BC，
∴ 四边形 ABCD 是平行四边形.
∵ ∠ABC = 90°，
∴ 四边形 ABCD 是矩形
(2)
∵ ∠BEC = 90°，F 是 BC 的中点，
∴ BF = CF = EF = 4.
∴ BC = 8.
∵ 四边形 ABCD 是矩形，
∴ ∠BCD = ∠D = 90°.
∵ ∠ECD = 30°，
∴ ∠BCE = 60°.
∴ △CEF 是等边三角形.
∴ EC = EF = 4.
∵ ∠D = 90°，∠ECD = 30°，
∴ ED = $\frac{1}{2}$EC = 2. 在Rt△EDC中，根据勾股定理，得 CD = $\sqrt{EC^2 - ED^2}$ = 2$\sqrt{3}$.
∴ 四边形 ABCD 的面积 = BC · CD = 8×2$\sqrt{3}$ = 16$\sqrt{3}$