第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1. 在一张复印出来的纸上,一个三角形的一条边由原图中的2cm增加了4cm,则该三角形的中线是原图中三角形对应中线的(
A.3倍
B.6倍
C.9倍
D.12倍
A
)A.3倍
B.6倍
C.9倍
D.12倍
答案:
1. A
2. (教材P108习题4.11第1题变式)如果两个相似三角形的对应高之比为2:5,其中一个三角形的一条角平分线的长为7,那么另一个三角形对应角平分线的长为(
A.$\frac{35}{2}$
B.$\frac{14}{5}$
C.$\frac{35}{2}$或$\frac{14}{5}$
D.无法确定
C
)A.$\frac{35}{2}$
B.$\frac{14}{5}$
C.$\frac{35}{2}$或$\frac{14}{5}$
D.无法确定
答案:
2. C
3. 如图所示为一个伸缩折叠的不锈钢晾衣架的侧面示意图,AD和CB相交于点O,点A,B之间的距离为1.2米,AB//CD,根据图中的数据,可得点C,D之间的距离为(
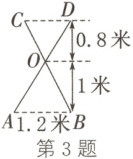
A.0.8米
B.0.86米
C.0.96米
D.1米
C
)
A.0.8米
B.0.86米
C.0.96米
D.1米
答案:
3. C
4. (教材P108随堂练习第2题变式)已知两个相似三角形对应角平分线的比为3:10,且这两个三角形的一对对应中线之差为56cm,则这两个三角形对应中线的长分别为
24cm,80cm
.
答案:
4. 24cm,80cm
5. (教材P108习题4.11第2题变式)(2023·山西模拟)如图,在测量凹透镜焦距时,将凹透镜嵌入直径为AB的圆形挡板中,用一束平行于凹透镜主光轴的光线射向凹透镜,在光屏上形成一个直径为CD的圆形光斑.测得凹透镜的光心O到光屏的距离OE=36cm,AB=20cm,CD=50cm,则凹透镜的焦距f为
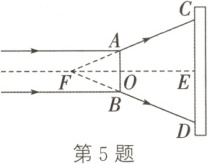
24
cm(f为焦点F到光心O的距离).
答案:
5. 24
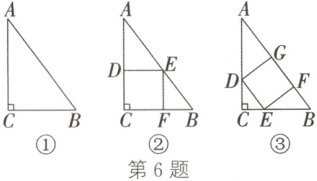
6. 有一批形状、大小相同的直角三角形不锈钢钢片.如图①,在△ABC中,∠C=90°,BC=3cm,AC=4cm,分别采取如图②③所示的两种方法截取一块正方形不锈钢钢片,且使正方形的面积较大.试判断哪种截法更好些,并说明理由.

答案:
6. 题图②的截法更好些 理由:设题图②中正方形的边长为 $x_1$cm. 由题意,易得 $\triangle ADE \sim \triangle EFB$. $\therefore \frac{AD}{EF} = \frac{DE}{FB}$. $\because BC = 3$cm,$AC = 4$cm, $\therefore \frac{4 - x_1}{x_1} = \frac{x_1}{3 - x_1}$, 解得 $x_1 = \frac{12}{7}$. 在题图③中过点 $C$ 作 $CM \perp AB$ 于点 $M$, 交 $DE$ 于点 $N$. 设题图③中正方形的边长为 $x_2$cm. $\because \angle ACB = 90°$,$BC = 3$cm,$AC = 4$cm, $\therefore$ 在 $Rt \triangle ABC$ 中,由勾股定理,得 $AB = \sqrt{AC^2 + BC^2} = 5$cm. $\therefore$ 易得 $CM = \frac{3 × 4}{5} = 2.4$(cm). 由题意,可知 $DE // AB$, $\therefore \angle CDE = \angle CAB$. $\because \angle DCE = \angle ACB$, $\therefore \triangle DCE \sim \triangle ACB$. $\therefore \frac{DE}{AB} = \frac{CN}{CM}$. $\therefore \frac{x_2}{5} = \frac{2.4 - x_2}{2.4}$, 解得 $x_2 = \frac{60}{37}$. $\therefore \frac{60}{37} \approx \frac{12}{7}$, $\therefore$ 题图②中正方形的面积较大. $\therefore$ 题图②的截法更好些.
查看更多完整答案,请扫码查看


