《2025年通成学典课时作业本九年级数学上册北师大版山西专版》

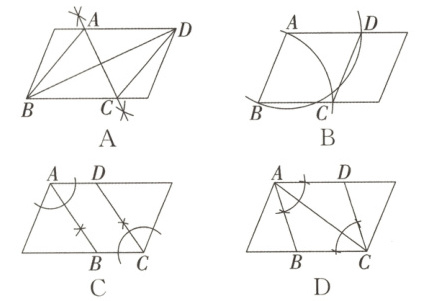
8. 若用尺规在一个平行四边形内作菱形$ABCD$，则下列作法中，错误的是(C)

答案： 8. C

9. (2022·泰安)如图，$□ ABCD$的对角线$AC$，$BD$相交于点$O$，$E$为$BC$的中点，连接$EO$并延长，交$AD$于点$F$，连接$AE$，$CF$，$\angle ABC = 60^{\circ}$，$BC = 2AB$。有下列结论：①$AB\perp AC$；②$AD = 4OE$；③四边形$AECF$是菱形；④$S_{\triangle BOE} = \frac{1}{4}S_{\triangle ABC}$。其中，正确的个数是(D)

A.1
B.2
C.3
D.4

答案： 9. D 解析：
∵ E为BC的中点，
∴ BC = 2BE = 2CE. 又
∵ BC = 2AB，
∴ AB = BE = CE.
∵ ∠ABC = 60°，
∴ △ABE是等边三角形.
∴ AE = BE = CE，∠BAE = ∠BEA = 60°.
∴ ∠EAC = ∠ECA.
∵ ∠BEA = ∠EAC + ∠ECA，
∴ ∠EAC = ∠ECA = 30°.
∴ ∠BAC = ∠BAE + ∠EAC = 90°，即AB⊥AC. 故①正确.
∵ 四边形ABCD是平行四边形，
∴ AD//BC，AD = BC，AO = CO.
∴ ∠CAD = ∠ACB.在△AOF和△COE中，
$\begin{cases} ∠OAF = ∠OCE \\ AO = CO \\ ∠AOF = ∠COE \end{cases}$
∴ △AOF ≌ △COE.
∴ AF = CE.
∵ AF// ∠AOF = ∠COE， CE，
∴ 四边形AECF是平行四边形.又
∵ AE = CE，
∴ 四边形AECF是菱形.故③正确.
∵ 四边形AECF是菱形，
∴ AC⊥EF.在Rt△COE中，
∵ ∠OCE = 30°，
∴$ OE = \frac{1}{2}CE = \frac{1}{4}BC = \frac{1}{4}AD. $
∴ AD = 4OE.故②正确.
∵ AO = CO，E为BC的中点，
∴$ S△BOE = \frac{1}{2}S△BOC = \frac{1}{4}S△ABC.$故④正确.

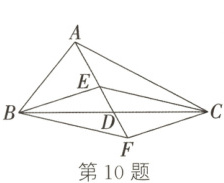
10. (2022·阳泉段考)如图，在$\triangle ABC$中，$D$是边$BC$的中点，点$E$，$F$分别在线段$AD$及$AD$的延长线上，且$DE = DF$。有下列条件：①$BE\perp EC$；②$BF// CE$；③$AB = AC$。其中，能判定四边形$BECF$是菱形的为③(填序号)。
]

答案： 10. ③

11. 如图，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = 4$，$BC = 3$，$D$为斜边$AB$上一点，以$CD$，$CB$为邻边作$□ CDEB$。当$AD = $\frac{7}{5}时，$□ CDEB$为菱形。

答案： $11. \frac{7}{5} $解析：连接CE，交DB于点O.根据勾股定理，得AB = 5.根据菱形的对角线互相垂直平分、菱形的邻边相等，得OD = OB，CD = CB.根据三角形的面积公式，得$OC = \frac{12}{5}.$根据勾股定理，得$OB = \frac{9}{5}.$由AD = AB - 2OB，得$AD = \frac{7}{5}.$

12. (2023·湘西)如图，四边形$ABCD$是平行四边形，$BM// DN$，分别交对角线$AC$于点$M$，$N$，连接$MD$，$BN$。
（1）求证：$\angle DMN = \angle BNM$；
（2）若$\angle BAC = \angle DAC$，求证：四边形$BMDN$是菱形。
]

答案： 12.
(1) 连接BD，交AC于点O.
∵ 四边形ABCD是平行四边形，
∴ OB = OD.
∵ BM//DN，
∴ ∠MBO = ∠NDO.又
∵ ∠BOM = ∠DON，
∴ △BOM ≌ △DON.
∴ BM = DN.
∴ 四边形BMDN为平行四边形.
∴ BN//DM.
∴ ∠DMN = ∠BNM
(2)
∵ 四边形ABCD是平行四边形，
∴ BC//AD.
∴ ∠BCA = ∠DAC.
∵ ∠BAC = ∠DAC，
∴ ∠BAC = ∠BCA.
∴ AB = BC.
∴ 四边形ABCD是菱形.
∴ AC⊥BD.
∴ MN⊥BD.由
(1)，知四边形BMDN为平行四边形，
∴ 四边形BMDN是菱形

13. 如图，在$□ ABCD$和$□ BFDE$中，$\angle A = \angle F$，$AD$与$BE$交于点$M$，$BC$与$DF$交于点$N$。
（1）求证：四边形$BNDM$是平行四边形。
（2）当$AB$与$FB$满足什么数量关系时，四边形$BNDM$是菱形？请说明理由。

答案： 13.
(1)
∵ 四边形ABCD和四边形BFDE都是平行四边形，
∴ BC//AD，BE//DF.
∴ 四边形BNDM是平行四边形
(2) 当AB = FB时，四边形BNDM是菱形 理由：
∵ BC//AD，BE//DF，
∴ ∠A + ∠ABC = 180°，∠EBF + ∠F = 180°.
∵ ∠A = ∠F，∠ABC = ∠EBF.
∴ ∠ABC - ∠EBC = ∠EBF - ∠EBC，即∠ABM = ∠FBN.在△ABM和△FBN中，
$\begin{cases} ∠ABM = ∠FBN \\ AB = FB \\ ∠A = ∠F \end{cases}$
(1)，得四边形BNDM是平行四边形，
∴ 四边形BNDM是菱形.