《2025年通成学典课时作业本九年级数学上册北师大版山西专版》

1. 如图，在$□ ABCD$中，有下列条件：①$AC=BD$；②$AB=AD$；③$\angle 1=\angle 2$；④$AB\perp BC$。其中，能判定$□ ABCD$是矩形的为(B)

A.①③
B.①④
C.②③
D.②④

答案： 1. B

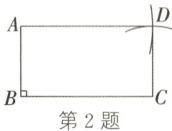
2. 如图，线段$AB\perp BC$，以点$C$为圆心，$BA$长为半径画弧，再以点$A$为圆心，$BC$长为半径画弧，两弧交于点$D$，连接$AD$，$CD$，则四边形$ABCD$是矩形，其依据是有一个角是直角的平行四边形是矩形。

答案： 2. 有一个角是直角的平行四边形是矩形

3. (2022·大同段考)如图，在$\triangle ABC$中，$D$，$E$分别是$AB$，$AC$的中点，点$F$，$G$在边$BC$上，且$DG=EF$。要使四边形$DFGE$是矩形，只需添加的一个条件是答案不唯一，如$DE=FG$。

答案： 3. 答案不唯一，如$DE=FG$

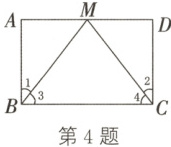
4. (教材P16随堂练习变式)(2023·岳阳)如图，点$M$在$□ ABCD$的边$AD$上，$BM=CM$，请从以下三个选项：①$\angle 1=\angle 2$；②$AM=DM$；③$\angle 3=\angle 4$中，选择一个合适的选项作为已知条件，使$□ ABCD$为矩形。
(1)你添加的条件是答案不唯一，如①(填序号)；
(2)添加条件后，请证明$□ ABCD$为矩形。

答案： 4. 答案不唯一，如
(1)①
(2)$\because$四边形$ABCD$是平行四边形，$\therefore AB// DC$，$AB = DC$。$\therefore \angle A + \angle D = 180^{\circ}$。在$\triangle ABM$和$\triangle DCM$中，
$\begin{cases}AB = DC,\\\angle 1 = \angle 2,\\BM = CM,\end{cases}$
$\therefore \triangle ABM \cong \triangle DCM$。$\therefore \angle A = \angle D$。
$\therefore \angle A = \angle D = 90^{\circ}$。$\therefore □ ABCD$为矩形

5. 如图，$BD$是$□ ABCD$的一条对角线，$E$是$CD$的中点，连接$AE$并延长，交$BC$的延长线于点$F$，连接$DF$。
（1）求证：$BC=FC$；
（2）当$DB=DF$时，求证：四边形$ABCD$是矩形。

答案： 5.
(1)$\because$在$□ ABCD$中，$AD// BC$，$AD = BC$，$\therefore \angle DAE = \angle CFE$。$\because E$是$CD$的中点，$\therefore DE = CE$。在$\triangle ADE$和$\triangle FCE$中，
$\begin{cases}\angle DAE = \angle CFE,\\\angle AED = \angle FEC,\\DE = CE,\end{cases}$
$\therefore \triangle ADE \cong \triangle FCE$。$\therefore AD = FC$。
$\therefore BC = FC$
(2)$\because DB = DF$，$\therefore \triangle BDF$是等腰三角形。
$\because BC = FC$，$\therefore DC\perp BC$。$\therefore \angle BCD = 90^{\circ}$。又$\because$四边形$ABCD$是平行四边形，$\therefore$四边形$ABCD$是矩形

6. 如图，$AD$是$\triangle ABC$的中线，四边形$ADCE$是平行四边形。小明说：“若$AB=AC$，则四边形$ADCE$是矩形。”小强说：“若$\angle BAC=90^{\circ}$，则四边形$ADCE$是菱形。”对于小明和小强的说法，下列判断正确的是(C)

A.小明的说法不对，小强的说法对
B.小明的说法对，小强的说法不对
C.小明和小强的说法都对
D.小明和小强的说法都不对

答案： 6. C

7. 如图，四边形$ABCD$为平行四边形，延长$AD$至点$E$，使$DE=AD$，连接$EB$，$EC$，$DB$，添加下列一个条件，其中，不能使四边形$DBCE$成为矩形的是(D)

A.$AB=BE$
B.$CE\perp DE$
C.$\angle ADB=90^{\circ}$
D.$BE\perp DC$

答案： 7. D