《2025年通成学典课时作业本九年级数学上册北师大版山西专版》

8. 如图，在$□ ABCD$中，$E$是$AD$的中点，$AC$与$BE$交于点$F$，过点$F$作$FG// BC$，交$AB$于点$G$。若$BC = 6$，则$FG$的长为(B)

A.$\frac {3}{2}$
B.2
C.$\frac {5}{2}$
D.$\frac {7}{4}$

答案： 8.B

9. 如图，在正方形$ABCD$中，$\triangle BPC$是等边三角形，$BP$，$CP$的延长线分别交$AD$于点$E$，$F$，连接$BD$，$DP$，$BD$与$CF$相交于点$H$。给出下列结论：①$BE = 2AE$；②$\triangle DFP\backsim\triangle BPH$；③$\triangle PFD\backsim\triangle PDB$；④$DP^{2} = PH· PC$。其中，正确的是(C)

A.①②③④
B.②③
C.①②④
D.①③④

答案： 9.C

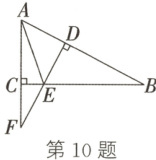
10. 如图，在$\triangle ABC$中，$∠ACB = 90^{\circ}$，$E$为$BC$上一点，过点$E$作$ED⊥AB$，垂足为$D$，延长$AC$，$DE$交于点$F$，连接$AE$。若$AE = 6$，$CE = 2$，则$\frac {CF}{BC}$的值为$\frac{\sqrt{2}}{4}$。

答案： 10.$\frac{\sqrt{2}}{4}$

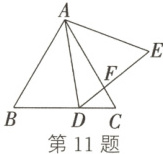
11. 如图，$\triangle ABC$和$\triangle ADE$都是等边三角形，点$D$在$BC$上，$DE$交$AC$于点$F$。若$DF = 2$，$EF = 4$，则$CD$的长是$\frac{6\sqrt{7}}{7}$。

答案： 11.$\frac{6\sqrt{7}}{7}$解析：根据△ABC和△ADE都是等边三角形，得出△ABD∽△DCF，△ADF∽△ACD，设CD = x，得到两个用x表示AF长的代数式，解方程可得CD的长。

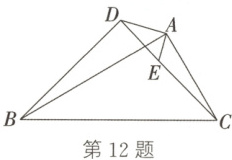
12. 如图，$\frac {AD}{AE}=\frac {AB}{AC}=\frac {BD}{CE}$。
（1）求证：$\triangle ADE\backsim\triangle ABC$；
（2）若$∠BAC = 90^{\circ}$，$AB = 6$，$BC = 3\sqrt {5}$，$AE = 1$，求$DE$的长。

答案： 12.（1）
∵$\frac{AD}{AE}=\frac{AB}{AC}=\frac{BD}{CE}$，
∴△BAD∽△CAE。
∴∠BAD = ∠CAE。
∴∠BAD + ∠BAE = ∠CAE + ∠BAE，即∠DAE = ∠BAC。
∵$\frac{AD}{AE}=\frac{AB}{AC}$，
∴$\frac{AD}{AB}=\frac{AE}{AC}$。
∴△ADE∽△ABC
（2）
∵∠BAC = 90°，AB = 6，BC =$3\sqrt{5}$，
∴在Rt△ABC中，由勾股定理，得$AC=\sqrt{BC^{2}-AB^{2}} = 3$。
∵△ADE∽△ABC，
∴$\frac{AE}{AC}=\frac{DE}{BC}$。
∴$\frac{1}{3}=\frac{DE}{3\sqrt{5}}$。
∴$DE=\sqrt{5}$

13. 如图，在等腰直角三角形$ABC$中，$∠BAC = 90^{\circ}$，$D$是边$AC$上一点，$AH⊥BD$于点$H$，连接$CH$。
（1）求证：$\triangle DAH\backsim\triangle DBA$。
（2）若$AC = 6$，点$D$在$AC$上运动，当点$D$运动到边$AC$的什么位置时，$∠DHC = 45^{\circ}$？请给出证明，并求出此时$CH$的长。

答案： 13.（1）
∵AH⊥BD，∠BAC = 90°，
∴∠AHD = ∠BAD = 90°。
∵∠ADH = ∠BDA，
∴△DAH∽△DBA（2）当点D运动到边AC的中点时，∠DHC = 45°由（1），知△DAH∽△DBA。
∴$\frac{DA}{DB}=\frac{DH}{DA}$。
∵D是AC的中点，
∴DA = DC。
∴$\frac{DC}{DB}=\frac{DH}{DC}$。
∵∠HDC = ∠CDB，
∴△DCH∽△DBC。
∴∠DHC = ∠DCB。
∵△ABC是等腰直角三角形，
∴∠DCB = 45°。
∴∠DHC = 45°。
∵△ABC是等腰直角三角形，AC = 6，
∴AB = 6，DA = DC = 3。在Rt△ABD中，根据勾股定理，得$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{6^{2}+3^{2}} = 3\sqrt{5}$。在Rt△ABC中，根据勾股定理，得$BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{6^{2}+6^{2}} = 6\sqrt{2}$。
∵△DCH∽△DBC，
∴$\frac{CH}{BC}=\frac{DC}{DB}$。
∴$\frac{CH}{6\sqrt{2}}=\frac{3}{3\sqrt{5}}$。
∴$CH=\frac{6\sqrt{10}}{5}$