2025年聚能闯关期末复习冲刺卷七年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年聚能闯关期末复习冲刺卷七年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
4. (10分)如图,某轮船上午8时在$A$处,测得灯塔$S$在北偏东$60^{\circ}$的方向上,向东行驶至中午12时,轮船到达$B$处,在$B$处测得灯塔$S$在北偏西$30^{\circ}$的方向上。已知轮船的行驶速度为20千米/时。
(1)在图中画出灯塔$S$的位置;
(2)量出轮船在$B$处时,离灯塔$S$的图上距离,并求出它的实际距离。
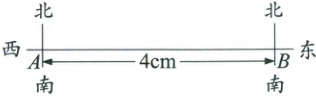
(1)在图中画出灯塔$S$的位置;
(2)量出轮船在$B$处时,离灯塔$S$的图上距离,并求出它的实际距离。

答案:
4.解:
(1)灯塔S的位置如图:

(2)量得图中BS=2cm。
轮船上午8时到中午12时行驶了4小时,
∴行驶的路程为20×4=80(千米)。
∵图中AB=4cm,
∴该图的比例尺为$\frac{4}{80×1000×100}$=$\frac{1}{2000000}$。
∴轮船在B处时离灯塔S的实际距离为2000000×2=4000000(厘米)=40千米。
4.解:
(1)灯塔S的位置如图:

(2)量得图中BS=2cm。
轮船上午8时到中午12时行驶了4小时,
∴行驶的路程为20×4=80(千米)。
∵图中AB=4cm,
∴该图的比例尺为$\frac{4}{80×1000×100}$=$\frac{1}{2000000}$。
∴轮船在B处时离灯塔S的实际距离为2000000×2=4000000(厘米)=40千米。
5. (10分)如图所示,从一点$O$出发,引两条射线可以得到1个角,引三条射线可以得到3个角,引四条射线可以得到6个角,引五条射线可以得到10个角。如果从一点出发引$n$($n$为大于等于2的整数)条射线,则会得到多少个角?当$n = 8$时,会得到多少个角?
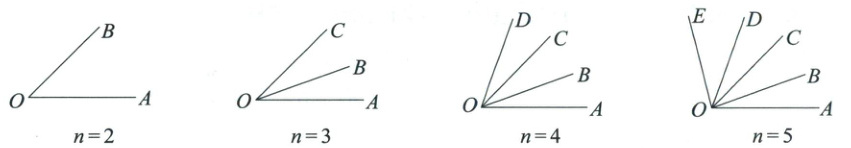
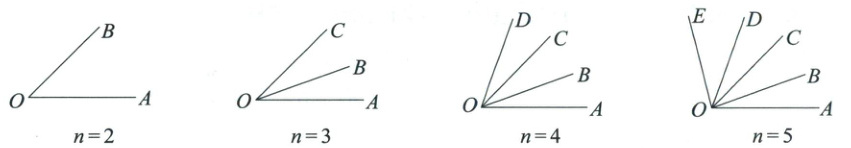
答案:
5.解:当n=2时,角的个数为1;
当n=3时,角的个数为1+2=3;当n=4时,角的个数为1+2+3=6;当n=5时,角的个数为1+2+3+4=10,
∴当射线的条数为n时,角的个数为1+2+3+4+…+(n−2)+(n−1)=$\frac{1}{2}$(n−1)n。
当n=8时,得到的角个数为$\frac{1}{2}$(n−1)n=
$\frac{1}{2}$×(8−1)×8=28(个)。
当n=3时,角的个数为1+2=3;当n=4时,角的个数为1+2+3=6;当n=5时,角的个数为1+2+3+4=10,
∴当射线的条数为n时,角的个数为1+2+3+4+…+(n−2)+(n−1)=$\frac{1}{2}$(n−1)n。
当n=8时,得到的角个数为$\frac{1}{2}$(n−1)n=
$\frac{1}{2}$×(8−1)×8=28(个)。
6. (10分)已知点$C$,$N$在射线$AB$上,$M$是线段$AC$的中点。
(1)如图,当点$C$在线段$AB$上时,若$N$是线段$CB$的中点,$AC = 10$,$BC = 14$,求线段$MN$的长;
(2)当点$C$在线段$AB$的延长线上时,若$CN:BN = 1:2$,$AC = a$,$BC = b$,直接写出线段$MN$的长(用含$a$,$b$的式子表示)。

(1)如图,当点$C$在线段$AB$上时,若$N$是线段$CB$的中点,$AC = 10$,$BC = 14$,求线段$MN$的长;
(2)当点$C$在线段$AB$的延长线上时,若$CN:BN = 1:2$,$AC = a$,$BC = b$,直接写出线段$MN$的长(用含$a$,$b$的式子表示)。

答案:
6.解:
(1)
∵M为线段AC的中点,N为线段BC 的中点,
∴CM=$\frac{1}{2}$AC=5,CN=$\frac{1}{2}$BC=7,
∴MN=CM+CN=5+7=12。
(2)如图。
∵M是线段AC的中点,
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}a$。
当点N在线段BC上时,
∵CN:BN=1:2,
∴CN=$\frac{1}{3}$BC=$\frac{1}{3}b$。
∴MN=CM−CN=$\frac{1}{2}a-\frac{1}{3}b$。
当点N在点C的右侧时,
∵CN:BN=1:2,
∴CN=BC=b。
∴MN=CM+CN=$\frac{1}{2}a+b$。
综上所述,线段MN的长为$\frac{1}{2}a-\frac{1}{3}b$或$\frac{1}{2}a+b$。
(1)
∵M为线段AC的中点,N为线段BC 的中点,
∴CM=$\frac{1}{2}$AC=5,CN=$\frac{1}{2}$BC=7,
∴MN=CM+CN=5+7=12。
(2)如图。
∵M是线段AC的中点,
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}a$。
当点N在线段BC上时,
∵CN:BN=1:2,
∴CN=$\frac{1}{3}$BC=$\frac{1}{3}b$。
∴MN=CM−CN=$\frac{1}{2}a-\frac{1}{3}b$。
当点N在点C的右侧时,
∵CN:BN=1:2,
∴CN=BC=b。
∴MN=CM+CN=$\frac{1}{2}a+b$。
综上所述,线段MN的长为$\frac{1}{2}a-\frac{1}{3}b$或$\frac{1}{2}a+b$。
查看更多完整答案,请扫码查看


