《2025年聚能闯关期末复习冲刺卷七年级数学上册浙教版》

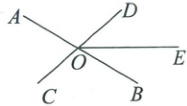
4. （10分）如图，直线$AB$，$CD$相交于点$O$，$\angle AOC = 70^{\circ}$，射线$OE$把$\angle BOD$分成两个角，且$\angle BOE:\angle EOD = 3:4$。
（1）求$\angle EOD$的度数；
（2）过点$O$作射线$OF\perp OE$，求$\angle DOF$的度数。

答案：
解:
(1)设∠BOE = 3x，则∠EOD = 4x。
　
∵∠AOC = 70°，
　
∴∠BOD = ∠AOC = 70°。
　
∵∠BOD = ∠BOE + ∠DOE，
　
∴3x + 4x = 70°。
　
∴x = 10°。
　
∴∠EOD = 4×10° = 40°。
(2)如图1。
　
∵OF⊥OE，
∴∠FOE = 90°。
　
∵∠EOD = 40°，
　
∴∠DOF = ∠FOE - ∠EOD = 90° - 40° = 50°。
　　　　如图2。
　
∵OF⊥OE，
∴∠FOE = 90°。
　
∵∠EOD = 40°，
　
∴∠DOF = ∠FOE + ∠EOD = 90° + 40° = 130°。
　
∴∠DOF的度数是50°或130°。
　　　　 　　

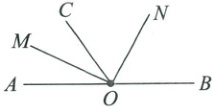
5. （12分）如图，$O$为直线$AB$上一点，$OM$是$\angle AOC$的平分线，$ON$是$\angle COB$的平分线。
（1）指出图中所有互为补角的角；
（2）求$\angle MON$的度数；
（3）指出图中所有互为余角的角。

答案： 解:
(1)∠AOM与∠MOB，∠AOC与∠BOC，∠AON与∠BON，∠COM与∠MOB，∠CON与∠AON。
(2)
∵OM是∠AOC的平分线，ON是∠BOC 的平分线，
　
∴∠COM = $\frac{1}{2}$∠AOC，∠CON = $\frac{1}{2}$∠BOC。
　
∵∠AOB = ∠AOC + ∠BOC = 180°，
　
∴∠MON = ∠COM + ∠CON
　　　　　　　 = $\frac{1}{2}$(∠AOC + ∠BOC)
　　　　　　　 = $\frac{1}{2}$×180°
　　　　　　　 = 90°。
(3)∠AOM与∠CON，∠AOM与∠BON，∠COM与∠CON，∠COM与∠BON。

6. （12分）如图，已知线段$AB$，按下列要求完成画图和计算：
（1）延长线段$AB$到点$C$，使$BC = 3AB$（尺规作图，不写作法，保留作图痕迹）；
（2）在（1）的条件下，如果$D$为线段$BC$的中点，且$AB = 2$，求线段$AD$的长度；
（3）在以上的条件下，若点$P$从$A$点出发，以每秒1个单位长度的速度向点$C$移动，到点$C$时停止。设点$P$的运动时间为$t$秒，是否存在某时刻$t$，使得$PB = PA - PC$？若存在，求出时间$t$；若不存在，请说明理由。

答案：
解:
(1)如图所示:
　　　　
(2)
∵AB = 2，
　
∴BC = 3AB = 6。
　
∵D为线段BC的中点，
　
∴BD = $\frac{1}{2}$BC = 3。
　
∴AD = AB + BD = 5。
(3)存在。
　　　　设点P的运动时间为t秒，
　　　　则PB = |t - 2|，PA = t，PC = 8 - t。
　
∵PB = PA - PC，
　
∴|t - 2| = t - (8 - t)。
　　　　解得t = 6或$\frac{10}{3}$。
　　　　但是当t = $\frac{10}{3}$时，PA - PC = t - (8 - t) = 2t - 8 = -$\frac{4}{3}$，不符合题意，舍去。
　　　　故当点P的运动时间t为6秒时，PB = PA - PC。