《2025年行知天下八年级数学上册青岛版》

10. 如图，已知线段$a$，$c$和$\angle \alpha$，用直尺和圆规作$\triangle ABC$，使$\angle ABC = \angle \alpha$，$AB = c$，$BC = a$.

答案：
10.解：如图所示，△ABC即为所求.

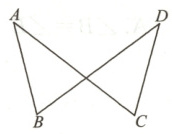
例题1 如图，已知$AB = DC$，$DB = AC$.
(1)试说明：$\angle ABD = \angle DCA$(说明过程要求给出每一步结论成立的依据)；
(2)在(1)的说明过程中，需要做辅助线，其意图是什么？

答案：
分析：
(1)连接$AD$，证明$\triangle BAD$和$\triangle CAD$全等，即可得到结论.
(2)作辅助线的意图是构造全等的三角形.

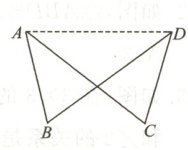
解：
(1)连接$AD$.
在$\triangle BAD$和$\triangle CDA$中，因为$AB = CD$(已知)，$DB = AC$(已知)，$AD = AD$(公共边)，
所以$\triangle BAD \cong \triangle CDA$(SSS)，
所以$\angle ABD = \angle DCA$(全等三角形对应角相等).
(2)作的辅助线为两个三角形的公共边，意图是构造全等的三角形.
点拨：作辅助线构造三角形是解答本题的关键，通过本题仔细体会辅助线在几何证明题中“牵线搭桥”的作用.