《2025年行知天下八年级数学上册青岛版》

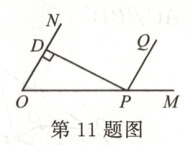
11.如图，点$P$是$\angle NOM$的边$OM$上一点，$PD\bot ON$于点$D$，$\angle OPD = 30^{\circ}$，$PQ// ON$，则$\angle MPQ$的度数是60° 

答案： 11.60°

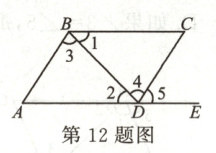
12.如图，点$E$在$AD$的延长线上，下列条件：①$\angle3 = \angle4$；②$\angle A + \angle ADC = 180^{\circ}$；③$\angle1 = \angle2$；④$\angle A = \angle5$；⑤$\angle C = \angle5$；⑥$\angle A = \angle C$.其中能判断$BC// AD$的有③⑤ 

答案： 12.③⑤

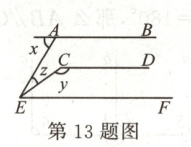
13.如图，已知$AB// CD// EF$，$\angle x = 80^{\circ}$，$\angle z = 25^{\circ}$，则$\angle y =$125° 

答案： 13.125°

14.如图，将一块含有$30^{\circ}$角的直角三角板的两个顶点叠放在矩形的两条对边上，如果$\angle1 = 27^{\circ}$，那么$\angle2$等于57° 

答案： 14.57°

15.用反证法证明“已知$a ＞ b$，$b ＞ c$，求证：$a ＞ c$.”第一步应先假设a≤c 

答案： 15.a≤c

16.如图，已知$AD\bot BC$，$EF\bot BC$，$\angle1 = \angle2$，试判断$DG$和$BA$的关系，并说明理由.

答案： 16.解：DG//BA.证明如下：
因为AD⊥BC,EF⊥BC(已知)，
所以∠ADC=∠EFC=90°(定义)，
所以AD//EF(同位角相等，两直线平行)，
所以∠1=∠BAD(两直线平行，同位角相等).
因为∠1=∠2(已知)，
所以∠2=∠BAD(等量代换)，
所以DG//BA(内错角相等，两直线平行).

17.如图，已知$\angle AFG = \angle C$，$\angle1 + \angle2 = 180^{\circ}$，求证：$BF// DE$.

答案： 17.证明：因为∠AFG=∠C，
所以FG//BC(同位角相等，两直线平行)，
所以∠1=∠3(两直线平行，内错角相等).
因为∠1+∠2=180°，
所以∠2+∠3=180°(等量代换)，
所以BF//DE(同旁内角互补，两直线平行).

18.如图，线段$AB$，$AD$交于点$A$，$C$为直线$AD$上一点（不与点$A$，$D$重合）.过点$C$在$BC$的右侧作射线$CE\bot BC$，过点$D$作直线$DF// AB$，交$CE$于点$G$（$G$与$D$不重合）.
(1)如图，若点$C$在线段$AD$上，且$\angle BCA$为钝角.求证：$\angle CGD - \angle B = 90^{\circ}$.
(2)若点$C$在线段$DA$的延长线上，直接写出$\angle B$与$\angle CGD$的数量关系.

答案：
18.
(1)证明：如图，过点C作CH//AB，
∴∠1=∠B.
∵AB//DF，
∴CH//DF，
∴∠2+∠HCG=180°.
∵CE⊥BC，
∴∠1+∠HCG=90°，
∴∠CGD+(90°-∠B)=180°，
即∠CGD-∠B=90°.

(2)∠CGD+∠B=90°.
理由：如图，过点C作CH//AB，
∴∠B=∠BCH.
∵AB//DF，
∴CH//DF，
∴∠CGD+∠HCG=180°.
又
∵CE⊥CB，
∴∠BCG=90°，
∴∠BCH+90°+∠CGD=180°，
即∠B+∠CGD=90°.