《2025年行知天下八年级数学上册青岛版》

19.如图，已知点$B$，$F$，$C$，$E$在同一条直线上，$FB = CE$，$AC = DF$.能否根据这些已知条件证明$AB// ED$？如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使$AB// ED$成立，并给出证明.
供选择的三个条件（请从其中选择一个）：①$AB = ED$；②$BC = EF$；③$\angle ACB = \angle DFE$.

答案： 19.解：若选择①，证明：因为FB=CE，所以FB+FC=CE+FC，即BC=EF.又因为AB=ED，AC=DF，所以△ABC≌△DEF，所以∠B=∠E，所以AB//ED.
若选择③，证明：因为FB=CE，所以FB+FC=CE+FC，即BC=EF.又因为∠ACB=∠DFE，AC=DF，所以△ABC≌△DEF，所以∠B=∠E，所以AB//ED.

20.如图，在$\triangle ABC$中，$AD$是$BC$边上的高，$CE$是$\angle ACB$的平分线，$\angle APE = 55^{\circ}$，$\angle AEP = 80^{\circ}$，求$\triangle ABC$各个内角的度数.

答案： 20.解：在△AEP中，∠APE=55°，∠AEP=80°，
所以∠EAP=180°-55°-80°=45°.
因为AD是BC边上的高，
所以△ABD是直角三角形，
所以∠B=45°.
在Rt△PDC中，∠CPD=∠APE=55°，
所以∠BCE=90°-55°=35°.
又因为CE是∠ACB的平分线，
所以∠ACB=2∠BCE=70°，
所以∠BAC=180°-45°-70°=65°.

21.如图，直线$AB// CD$，直线$EF$分别与$AB$，$CD$交于点$O$，$O'$.请用反证法证明：$\angle1 = \angle2$.

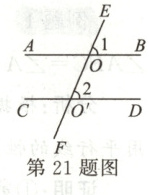
答案：
21.证明：假设∠1≠∠2.
如图，过点O作直线A'B'，使∠EOB'=∠2，
∴A'B'//CD(同位角相等，两直线平行).
∵AB//CD，且直线AB经过点O，
∴过点O存在两条直线AB，A'B'与直线CD平行.
这与基本事实过直线外一点有且只有一条直线与已知直线平行矛盾，假设不成立，
∴∠1=∠2.

如图(1)，线段$AB$，$CD$相交于点$O$，连接$AD$，$CB$，我们把形如图(1)的图形称之为“8字形”.如图(2)，在图(1)的条件下，$\angle DAB$和$\angle BCD$的平分线$AP$和$CP$相交于点$P$，并且与$CD$，$AB$分别相交于$M$，$N$.试解答下列问题：
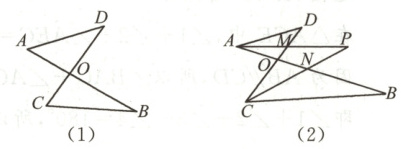
(1)在图(1)中，请直接写出$\angle A$，$\angle B$，$\angle C$，$\angle D$之间的数量关系：∠A+∠D=∠C+∠B ；
(2)仔细观察，图(2)中“8字形”的个数是：6个 ；
(3)在图(2)中，若$\angle D = 40^{\circ}$，$\angle B = 36^{\circ}$，试求$\angle P$的度数.

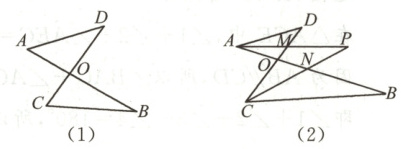
答案： 解：
(1)∠A+∠D=∠C+∠B
(2)①线段AB，CD相交于点O，形成“8字形”；②线段AN，CM相交于点O，形成“8字形”；③线段AB，CP相交于点N，形成“8字形”；④线段AB，CM相交于点O，形成“8字形”；⑤线段AP，CD相交于点M，形成“8字形”；⑥线段AN，CD相交于点O，形成“8字形”。
故“8字形”共有6个.
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
因为∠DAB和∠BCD的平分线AP和CP相交于点P，
所以∠DAP=∠PAB，∠DCP=∠PCB.
由①+②得：
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P，
即2∠P=∠D+∠B.
又∠D=40°，∠B=36°，
所以2∠P=40°+36°=76°，
所以∠P=38°.