《2025年同步练习册山东教育出版社七年级数学上册鲁教版五四制》

15. (10分)为迎接植树节的到来,红岩村街道准备对一块四边形空地$ABCD$进行绿化改造,某校数学兴趣小组的同学们帮助街道工作人员测量得到以下数据：$AB = 15$m,$CD = 8$m,$AD = 17$m。从点$A修一条垂直BC的小路AE$(垂足为$E$),$AE = 12$m,且$E恰好是BC$的中点。

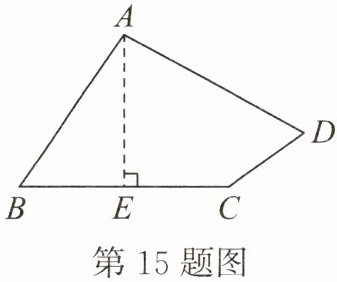
(1)求$BC$边的长；
(2)求空地$ABCD$的面积。

答案： （1）因为$AE\perp BC$，所以$\angle AEB=90^{\circ}$，
所以$\triangle ABE$是直角三角形。
在$Rt\triangle ABE$中，$AB = 15\ m$，$AE = 12\ m$，
由勾股定理得$BE^{2}=AB^{2}-AE^{2}=15^{2}-12^{2}=9^{2}$，
所以$BE = 9\ m$。
因为$E$是$BC$的中点，
所以$BC = 2BE = 18\ m$。
（2）如图，连接$AC$。
因为$AE\perp BC$，$E$是$BC$的中点，
所以$AE$是$BC$的垂直平分线，
所以$AC = AB = 15\ m$。
因为$AD = 17\ m$，$CD = 8\ m$，
所以$CD^{2}+AC^{2}=AD^{2}$，
所以$\triangle ACD$是直角三角形，$\angle ACD = 90^{\circ}$，
所以$S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ACD}=\dfrac{1}{2}×18×12+\dfrac{1}{2}×15×8=168(m^{2})$，
即空地$ABCD$的面积为$168\ m^{2}$。

16. (10分)如图,在长方体$ABCD - A'B'C'D'$中,$AB = BB' = 2$,$AD = 3$,一只蚂蚁从点$A$出发,沿长方体表面爬到点$C'$,蚂蚁怎样走路程最短？最短路程是多少？

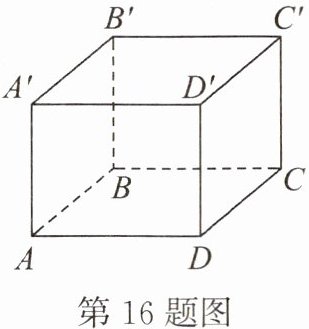
答案： 蚂蚁沿如图1所示的路线爬行时，长方形$ACC'A'$的长为$AD + DC = 5$，宽为$AA' = 2$。
连接$AC'$，则构成直角三角形$ACC'$。
由勾股定理，得$AC'^{2}=AC^{2}+CC'^{2}=5^{2}+2^{2}=29$。
蚂蚁沿如图2所示的路线爬行时，长方形$ADC'B'$的长为$DD'+D'C' = 4$，宽为$AD = 3$，连接$AC'$，则构成直角三角形$ADC'$。
由勾股定理，得$AC'^{2}=AD^{2}+DC'^{2}=3^{2}+4^{2}=25$，$AC' = 5$。
蚂蚁沿如图3所示的路线爬行时，长方形$ABC'D'$的长为$BB'+B'C' = 5$，宽为$AB = 2$，连接$AC'$，则构成直角三角形$ABC'$。
由勾股定理，得$AC'^{2}=AB^{2}+BC'^{2}=2^{2}+5^{2}=29$。
所以蚂蚁从点$A$出发穿过$A'D'$到达点$C'$时路程最短，最短路程是$5$。

17. (10分)台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力。如图1所示,有一台风中心沿东西方向$AB由A向B$移动,已知点$C$为一海港,且点$C与直线AB上的两点A$,$B的距离分别为AC = 300$km,$BC = 400$km,又$AB = 500$km,以台风中心为圆心周围250 km以内为受影响区域。

(1)求$\angle ACB$的度数。
(2)海港$C$受台风影响吗？为什么？
(3)如图2所示,若台风的速度为20 km/h,当台风运动到点$E$处时,海港$C$刚好受到影响,当台风运动到点$F$时,海港$C$刚好不受影响,即$CE = CF = 250$km,则台风影响该海港持续的时间有多长？

答案： （1）因为$300^{2}+400^{2}=500^{2}$，
即$AC^{2}+BC^{2}=AB^{2}$，
所以$\triangle ABC$是直角三角形，
所以$\angle ACB = 90^{\circ}$。
（2）海港$C$受台风影响。理由如下：
如图，过点$C$作$CD\perp AB$于点$D$。
由（1）知$\triangle ABC$是直角三角形，
所以$AC\cdot BC = CD\cdot AB$，
所以$300×400 = 500CD$，
所以$CD = 240\ km$。
因为以台风中心为圆心周围$250\ km$以内为受影响区域，$240 ＜ 250$，
所以海港$C$受台风影响。
（3）当$EC = 250\ km$，$FC = 250\ km$时，正好影响海港$C$，
所以$ED = 70(km)$，
所以$EF = 140\ km$。
因为台风的速度为$20\ km/h$，
所以$140÷20 = 7(h)$。
所以台风影响该海港持续的时间为$7\ h$。