2. 甲、乙、丙、丁、戊五位同学,他们的年龄之间的关系:丙没有丁大,乙比甲大,戊不比丁小,而乙不比丙大。那么年龄最小的是 ( )
A.甲
B.乙
C.丙
D.丁
A.甲
B.乙
C.丙
D.丁
答案:
A
3. 在如图所示的三个三角形中,面积最大的是______。
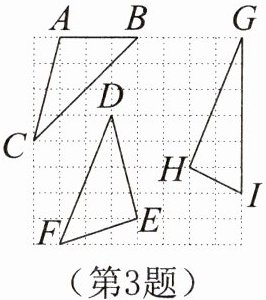

答案:
$\triangle DEF$。
4. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,若∠ABP= 20°,∠ACP= 50°,则∠A+∠P= ______。
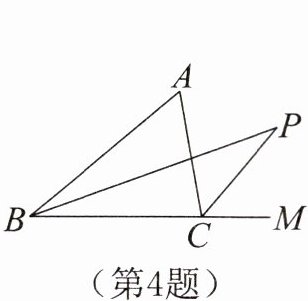

答案:
$90^\circ$。
5. 如图,在△ABC的三边上有D,E,F三点,点G在线段DF上,∠1与∠2互补,∠3= ∠C。
(1)若∠C= 40°,求∠BFD的度数;
(2)求证:DE//BC。
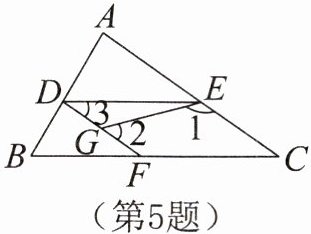
(1)若∠C= 40°,求∠BFD的度数;
(2)求证:DE//BC。

答案:
(1)$40^\circ$;
(2)略。
(1)$40^\circ$;
(2)略。
6. 如图,在△ABC中,已知CE平分∠ACB交AB于点E,且CE⊥AB,过点E作ED//AC交BC于点D,同时过点D作DF⊥AB于点F。求证:DF平分∠BDE。
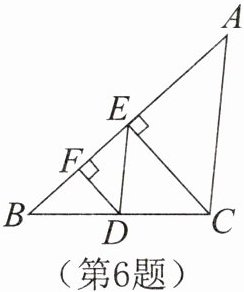

答案:
证明:
∵CE平分∠ACB,
∴∠ACE=∠BCE。
∵CE⊥AB,
∴∠AEC=∠BEC=90°。
在△AEC和△BEC中,
∠ACE=∠BCE,CE=CE,∠AEC=∠BEC,
∴△AEC≌△BEC(ASA),
∴AE=BE。
∵ED//AC,
∴∠DEC=∠ACE(内错角相等),∠BDE=∠ACB(同位角相等)。
∵∠ACE=∠BCE,
∴∠DEC=∠BCE,
∴ED=CD。
∵ED//AC,
∴∠BED=∠A,∠BDE=∠ACB。
∵△AEC≌△BEC,
∴AC=BC,
∴∠A=∠B,
∴∠BED=∠B,
∴ED=BD。
∵ED=CD,ED=BD,
∴BD=CD,即D为BC中点。
∵DF⊥AB,CE⊥AB,
∴DF//CE,
∴∠FDE=∠DEC,∠BDF=∠BCE。
∵∠DEC=∠BCE,
∴∠FDE=∠BDF,
∴DF平分∠BDE。
∵CE平分∠ACB,
∴∠ACE=∠BCE。
∵CE⊥AB,
∴∠AEC=∠BEC=90°。
在△AEC和△BEC中,
∠ACE=∠BCE,CE=CE,∠AEC=∠BEC,
∴△AEC≌△BEC(ASA),
∴AE=BE。
∵ED//AC,
∴∠DEC=∠ACE(内错角相等),∠BDE=∠ACB(同位角相等)。
∵∠ACE=∠BCE,
∴∠DEC=∠BCE,
∴ED=CD。
∵ED//AC,
∴∠BED=∠A,∠BDE=∠ACB。
∵△AEC≌△BEC,
∴AC=BC,
∴∠A=∠B,
∴∠BED=∠B,
∴ED=BD。
∵ED=CD,ED=BD,
∴BD=CD,即D为BC中点。
∵DF⊥AB,CE⊥AB,
∴DF//CE,
∴∠FDE=∠DEC,∠BDF=∠BCE。
∵∠DEC=∠BCE,
∴∠FDE=∠BDF,
∴DF平分∠BDE。
1. 张老师把红、白、蓝各一个气球分别送给三个小朋友。根据下面三句话,请你猜一猜,他们分到的各是什么颜色的气球?
(1)小春说:“我分到的不是蓝气球。”
(2)小宇说:“我分到的不是白气球。”
(3)小华说:“我看见张老师把蓝气球和红气球分给上面两位小朋友了。”
则小春、小宇、小华分别分到______颜色的气球。
(1)小春说:“我分到的不是蓝气球。”
(2)小宇说:“我分到的不是白气球。”
(3)小华说:“我看见张老师把蓝气球和红气球分给上面两位小朋友了。”
则小春、小宇、小华分别分到______颜色的气球。
答案:
红、蓝、白。
2. 已知α,β是两个钝角,计算1/6(α+β)的值。甲、乙、丙、丁四位同学算出了四种不同的答案分别为24°,48°,76°,86°,其中只有一个答案是正确的,则正确的答案是______。
答案:
$48^\circ$。
查看更多完整答案,请扫码查看


