《2025年课前课后快速检测八年级数学上册浙教版》

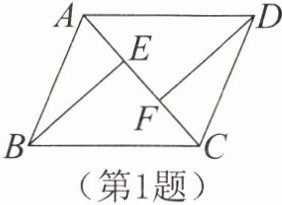
1. 如图,$AE= CF$,$BE= DF$,要说明$\triangle ABE \cong \triangle CDF$,还需添加的条件是( )

A.$\angle ABE= \angle CDF$
B.$\angle BAC= \angle ACD$
C.$\angle AEB= \angle CFD$
D.$\angle DAC= \angle BCA$
]

答案： C

2. 根据下列条件能画出唯一$\triangle ABC$的是( )

A.$AB= 1$,$BC= 2$,$CA= 3$
B.$AB= 7$,$BC= 5$,$\angle A= 30^\circ$
C.$\angle A= 50^\circ$,$\angle B= 60^\circ$,$\angle C= 70^\circ$
D.$AC= 3.5$,$BC= 4.8$,$\angle C= 70^\circ$

答案： D

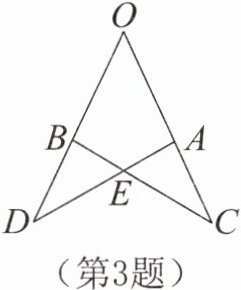
3. 如图,$OA= OB$,$OC= OD$,$\angle O= 50^\circ$,$\angle D= 35^\circ$,则$\angle AEC= $______°。
]

答案： 60。

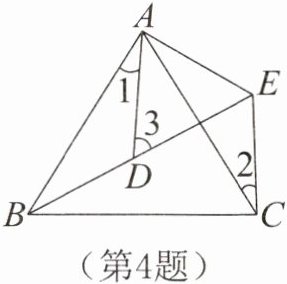
4. 如图所示,$AB= AC$,$AD= AE$,$\angle BAC= \angle DAE$,$\angle 1= 28^\circ$,$\angle 2= 30^\circ$,则$\angle 3$的度数为______。
]

答案： 58°。

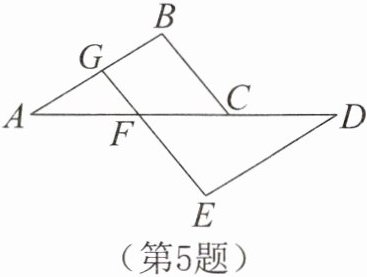
5. 如图所示,$F$,$C是AD$上两点,且$AF= CD$,点$E$,$F$,$G$在同一直线上,$\angle B= \angle AGF$,$BC= EF$。求证：$\triangle ABC \cong \triangle DEF$。
]

答案： 证明：
∵AF=CD，
∴AF+FC=CD+FC，即AC=DF。
∵点E，F，G在同一直线上，
∴∠AGF=∠DFE（对顶角相等）。
∵∠B=∠AGF，
∴∠B=∠DFE。
在△ABC和△DEF中，
$\begin{cases} ∠B=∠DFE \\BC=EF \\AC=DF \end{cases}$
∴△ABC≌△DEF（SAS）。

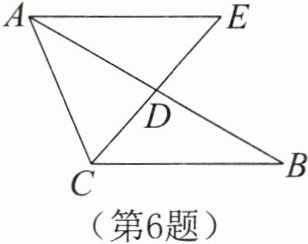
6. 如图所示,把$\triangle ABC的中线CD延长到点E$,使$DE= CD$,连结$AE$,若$AC= 4且\triangle BCD的周长比\triangle ACD$的周长大1,求$AE$的长度。
]

答案： 5。

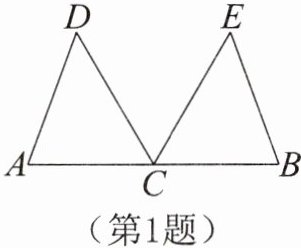
1. 如图,$C是AB$的中点,$CD平分\angle ACE$,$CE平分\angle BCD$,$CD= CE$。
(1)求证：$\triangle ACD \cong \triangle BCE$；
(2)若$\angle A-\angle E= 20^\circ$,求$\angle B$的度数。
]

答案：
(1)略；
(2)70°。

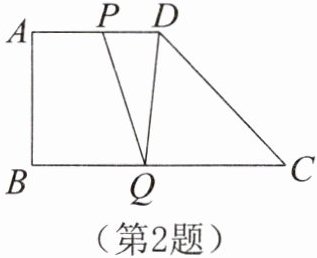
2. 如图,在四边形$ABCD$中,$AD // BC$,$\angle ABC= 90^\circ$,$AD= 12$,$BC= 24$,动点$P从点A$出发以每秒1个单位的速度沿$AD向点D$运动,动点$Q从点C$出发以每秒2个单位的速度沿$CB向点B$运动,点$P$,$Q$同时出发,当点$P$停止运动时,点$Q$也随之停止,连结$PQ$,$DQ$。设点$P运动时间为t$秒,问当$t$为何值时,$\triangle PDQ \cong \triangle CQD$,并证明$\triangle PDQ \cong \triangle CQD$。
]

答案： 由题意得AP=t,CQ=2t，
∵AD=12，
∴DP=12-t，当DP=QC时列方程，即12-t=2t，解得t=4，即当t=4时，△PDQ≌△CQD，
∴当t=4时，△PDQ≌△CQD，理由如下：
∵AD//BC，
∴根据平行线的性质，∠PDQ=∠CQD，在△PDQ和△CQD中，{DP=QC∠PDQ=∠CQD，
∴△PDQ≌△CQD(SAS)。DQ=QD