《2025年课前课后快速检测八年级数学上册浙教版》

2. 某平板电脑支架如图所示,其中EA= ED,为了使用的舒适性,可调整∠AEC的大小。若∠AEC增大16°,则∠BDE的变化情况是( )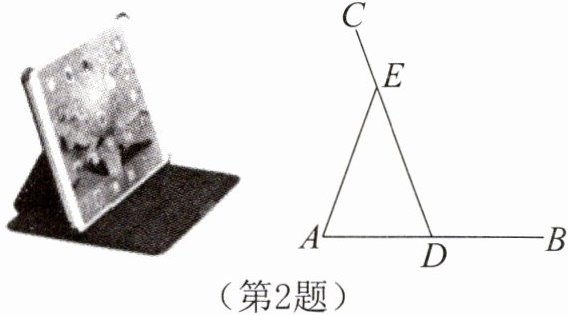

A.增大16°
B.减小16°
C.增大8°
D.减小8°

答案： D

3. 如图,在△ABC中,AB= AC,以B为圆心,BC的长为半径画弧交AC于点C,E,再分别以C,E为圆心,大于CE长的一半为半径画弧,两弧交于点F,连结BF交AC于点D,若∠A= 40°,则∠EBD是______。

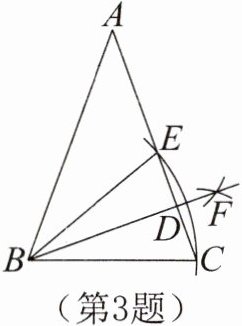
答案： 20°

4. 如图,在△ABC中,D,E分别为AB,AC边上的点,DA= DE,DB= BE= EC。若∠ABC= 130°,则∠C的度数为______。

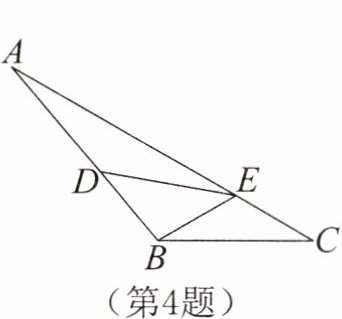
答案： 30°

5. 如图,已知△ABC是等边三角形,延长CB至点E,在线段EC外取一点D使得DE= DC,DC与AB相交于点F,若∠DFB= 2∠DCA,求∠DEC的度数。

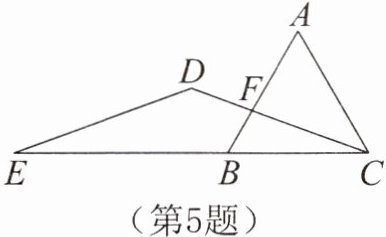
答案： 20°

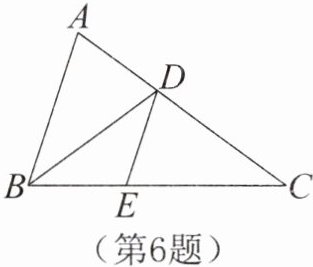
6. 如图,在△ABC中,点D,E分别在AC,BC上,连结BD,DE。已知∠ABC= 2∠C,BD= CD。
(1)若∠A= ∠DEC,求证：AB= EC；
(2)若AB= BD,求∠A的度数。

答案：
(1)略；
(2)72°

1. 如图,在△ABC中,D,E为BC边上两点,且满足AB= BE,AC= CD,连结AD,AE。如果∠BAC= 100°,那么∠DAE的度数为( )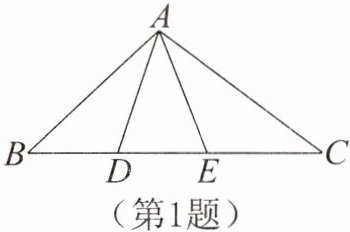

A.45°
B.40°
C.35°
D.30°

答案： B

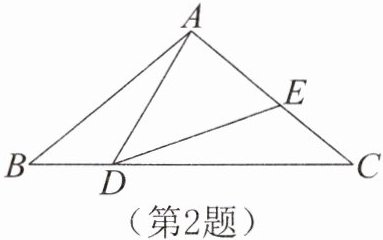
2. 如图所示,在△ABC中,AB= AC,∠B= 40°,点D在线段BC上运动(点D不与点B,C重合),连结AD,作∠ADE= 40°,DE交线段AC于点E,在点D的运动过程中,△ADE的形状也在改变。当△ADE是等腰三角形时,求∠BDA的度数。

答案：
∵AB=AC，
∴∠B=∠C=40°，①当AD=AE时，∠ADE=∠AED=40°，
∵∠AED＞∠C，
∴此时不符合；②当DA=DE时，即∠DAE=∠DEA=$\frac{1}{2}(180^{\circ}-40^{\circ})$=70°，
∵∠BAC=180°-40°-40°=100°，
∴∠BAD=100°-70°=30°，
∴∠BDA=180°-30°-40°=110°；③当EA=ED时，∠ADE=∠DAE=40°，
∴∠BAD=100°-40°=60°，
∴∠BDA=180°-60°-40°=80°，
∴当△ADE是等腰三角形时，∠BDA的度数是110°或80°。