《2025年课前课后快速检测八年级数学上册浙教版》

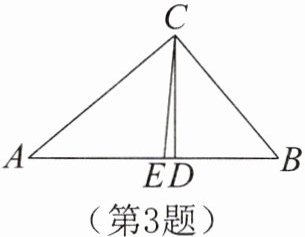
3. 如图,在△ABC中,∠ACB= 90°,∠B= 50°,CD是△ABC的高线,CE是△ABC的角平分线,那么∠DCE= ______°。

答案： 5

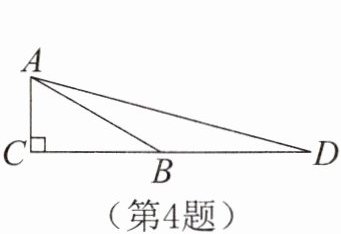
4. 如图,在△ABC中,∠ACB= 90°,∠D= 15°,AC= 2,AB= BD,则BD= ______。

答案： 4

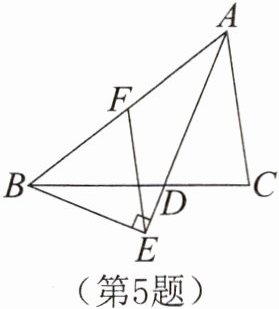
5. 如图,AD是△ABC的角平分线,过点B向AD的延长线作垂线,垂足为E,F是AB的中点。求证：EF//AC。

答案： 【解析】：本题考查直角三角形的性质以及平行线的判定条件。根据已知条件，$AD$是$\bigtriangleup ABC$的角平分线，所以$\angle BAD = \angle CAD$，又因为$BE$垂直于$AE$，所以$\bigtriangleup ABE$是直角三角形，根据直角三角形斜边中线定理，得出$EF = \frac{1}{2}AB = AF$，进而推出$\angle FEA = \angle FAE$，最后根据内错角相等，两直线平行，证明$EF// AC$。
【答案】：证明：
∵$AE \perp BE$，$F$是$AB$的中点，
∴在$Rt \bigtriangleup ABE$中，$EF = \frac{1}{2}AB = AF$，（直角三角形斜边中线等于斜边的一半）
∴$\angle FEA = \angle FAE$。（等边对等角）
∵$AD$是$\bigtriangleup ABC$的角平分线，
∴$\angle BAD = \angle CAD$，
∴$\angle FEA = \angle CAD$，
∴$EF// AC$。（内错角相等，两直线平行）

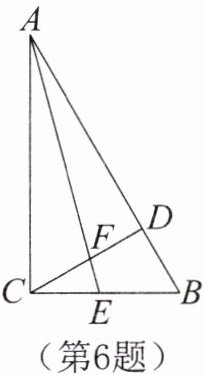
6. 如图所示,在△ABC中,∠ACB= 90°,CD是高,AE是△ABC内部的一条线段,AE交CD于点F,交CB于点E,且∠CFE= ∠CEF。求证：AE平分∠CAB。

答案： 证明：
∵∠ACB=90°，CD是高，
∴∠ACD+∠BCD=90°，∠B+∠BCD=90°，
∴∠ACD=∠B（同角的余角相等）。
∵∠CFE=∠CEF，∠CFE=∠AFD（对顶角相等），
∴∠CEF=∠AFD。
∵∠CEF=∠B+∠BAE，∠AFD=∠ACD+∠CAE，
∴∠B+∠BAE=∠ACD+∠CAE。
∵∠ACD=∠B，
∴∠BAE=∠CAE，
即AE平分∠CAB。

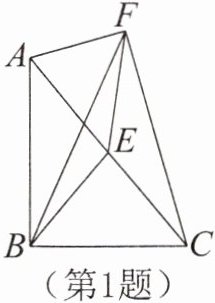
1. 如图,在△ABC中,∠ABC= 90°,E为AC的中点,在△AFC中,∠AFC= 90°,连结BE,BF,EF,若∠ACB= 50°,∠ECF= 24°,则∠EFB的度数为( )

A.14°
B.16°
C.18°
D.20°

答案： B

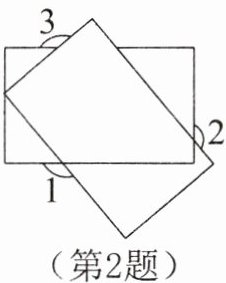
2. 如图是叠放在一起的两张长方形卡片,则图中相等的角是( )

A.∠1与∠2
B.∠2与∠3
C.∠1与∠3
D.三个角都相等

答案： B