《2025年课前课后快速检测八年级数学上册浙教版》

3. 若不等式组$\begin{cases}2x - 1 ＞ 3(x - 1) \\ x ＜ m\end{cases} 的解集是x ＜ 2$,则m的取值范围是______。

答案： m≥2。

4. 已知关于x的不等式组$\begin{cases}2x + a \geq 0 \\ 3x - 3 ＜ 9\end{cases} $恰好有3个整数解,则a的取值范围是______。

答案： -2＜a≤0。

5. 一幢学生宿舍楼有一些空宿舍,现有一批学生要入住,若每间住5人,则有25人无法入住；若每间住10人,则有1间房不空也不满。求空宿舍的间数和这批学生的人数。

答案： 6间，55人。

6. 若a,b,c是△ABC的三边,且a,b满足关系式$|a - 6| + (b - 8)^2 = 0$,c是不等式组$\begin{cases}\frac{2x + 5}{4} ＞ x - 4 \\ x + 2 ＜ \frac{4x + 1}{3}\end{cases} $的最大整数解,试判断△ABC的形状。

答案： |a-6|+(b-8)$^{2}$=0，
∴a-6=0，b-8=0，
∴a=6，b=8。
∵由不等式组$\left\{\begin{array}{l} \frac{2x+5}{4}＞x-4\\ x+2＜\frac{4x+1}{3}\end{array}\right.$的解得5＜x＜$\frac{21}{2}$，
∵c是不等式组$\left\{\begin{array}{l} \frac{2x+5}{4}＞x-4\\ x+2＜\frac{4x+1}{3}\end{array}\right.$的最大整数解，
∴c=10。
∵6$^{2}$+8$^{2}$=10$^{2}$，即a$^{2}$+b$^{2}$=c$^{2}$，
∴△ABC是直角三角形。

1. 已知a,b满足$3a + 2b = a + b + 3$,当$0 \leq a ＜ 2$时,则整数b有(　　)

A.2个　
B.3个　
C.4个　
D.5个

答案： C

2. 运行程序如图所示,规定：从“输入一个值x”到“结果是否＞94”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是______。

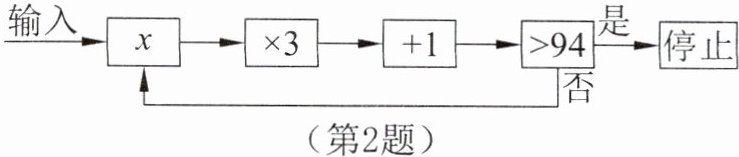
答案： 3＜x＜10。