《2025年课前课后快速检测八年级数学上册浙教版》

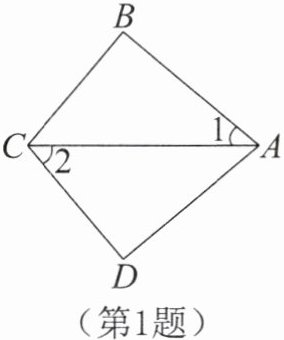
1.如图,∠B= ∠D= 90°,BC= CD,∠1= 40°,则∠2= ( )

A.40°
B.50°
C.60°
D.75°

答案： B

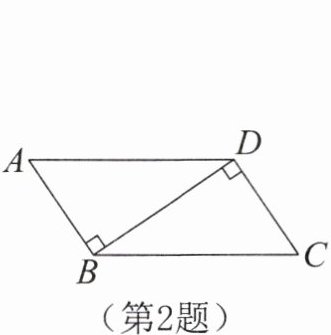
2.如图所示,已知AB⊥BD,CD⊥BD,AD= BC,判定Rt△ABD和Rt△CDB全等的依据是( )

A.AAS
B.SAS
C.ASA
D.HL

答案： D

3.下列条件中,不能判定两个直角三角形全等的是( )

A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.面积相等

答案： D

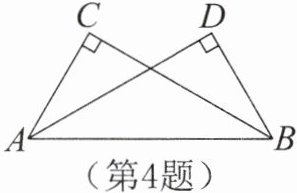
4.如图,AC⊥BC,AD⊥BD,垂足分别是C,D,若要用“HL”得到Rt△ABC≌Rt△BAD,则需添加的条件是______。(写一种即可)

答案： AC=BD。

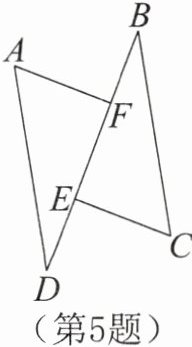
5.如图所示,已知点E,F在线段BD上,AF⊥BD,CE⊥BD,且AD= CB,DE= BF= 3,AF= 4,那么CE= ______。

答案： AF。

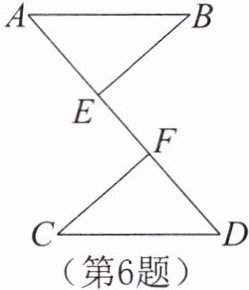
6.如图,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定Rt△ABE≌Rt△DCF的是______。(填序号)
①AB= DC,∠B= ∠C；②AB= DC,AB//CD；③AB= DC,BE= CF；④AB= DF,BE= CF。

答案： ①②③。

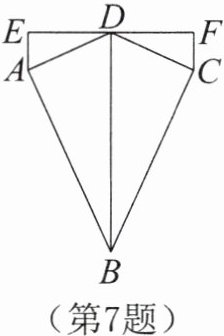
7.如图,AB= BC,∠BAD= ∠BCD= 90°,D是EF上一点,AE⊥EF于点E,CF⊥EF于点F,AE= CF,连结BD,求证：ED= DF。

答案： 【解析】：本题考查了直角三角形全等（HL）的判定方法，直角三角形中一条直角边和斜边对应相等的两个直角三角形全等。利用已知条件，先证明$Rt\bigtriangleup ABD$和$Rt\bigtriangleup CBD$全等，得出$AD = CD$，再证明$Rt\bigtriangleup ADE$和$Rt\bigtriangleup CDF$全等，从而证明$ED = DF$。
【答案】：证明：
∵$AB = BC$，$\angle BAD = \angle BCD = 90^{\circ}$，$BD = BD$，
∴$Rt\bigtriangleup ABD\cong Rt\bigtriangleup CBD(HL)$，
∴$AD = CD$，
∵$AE\perp EF$，$CF\perp EF$，
∴$\angle E = \angle F = 90^{\circ}$，
又
∵$AE = CF$，
∴$Rt\bigtriangleup ADE\cong Rt\bigtriangleup CDF(HL)$，
∴$ED = DF$。