《2025年课前课后快速检测八年级数学上册浙教版》

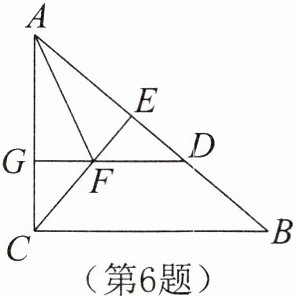
6. 如图,在$\triangle ABC$中,$\angle ACB= 90^\circ$,$CE \perp AB于点E$,$AD= AC$,$AF平分\angle CAB交CE于点F$,$DF的延长线交AC于点G$。
(1)求证：$DF // BC$；
(2)求证：$FG= FE$。

答案：
(1)证明：
∵AF平分∠CAB，
∴∠CAF=∠DAF，
在△ACF和△ADF中，
AC=AD，∠CAF=∠DAF，AF=AF，
∴△ACF≌△ADF(SAS)，
∴∠ACF=∠ADF，
∵∠ACB=90°，CE⊥AB，
∴∠ACE+∠CAE=90°，∠B+∠CAE=90°，
∴∠ACE=∠B，
∴∠ADF=∠B，
∴DF//BC.
(2)证明：
∵DF//BC，∠ACB=90°，
∴∠AGD=∠ACB=90°，即FG⊥AC，
∵CE⊥AB，AF平分∠CAB，
∴FG=FE.

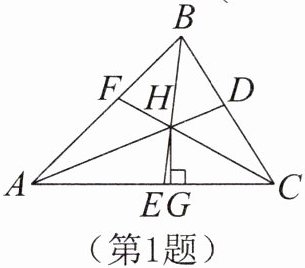
1. 如图,在$\triangle ABC$中,角平分线$AD$,$BE$,$CF相交于点H$,过点$H作HG \perp AC$,垂足为$G$,则$\angle AHE和\angle CHG$的大小关系为( )

A.$\angle AHE＞\angle CHG$
B.$\angle AHE＜\angle CHG$
C.$\angle AHE= \angle CHG$
D.不一定

答案： C

2. 已知$AD是\triangle ABC$的高,$\angle BAD= 62^\circ$,$\angle CAD= 28^\circ$,则$\triangle ABC$是什么三角形？

答案： △ABC是直角三角形或钝角三角形。