7. 举反例说明命题“对于任意实数$x$,$x^2+6x+8$的值都大于0”是假命题。
答案:
答案不唯一,如x=-2。
8. 如图,在$\triangle ABC$中,$AD平分\angle BAC$,$DF \perp AB$,$E是BC$的中点,连结$AE$,若$DF= 2$,$AC= 7$,$S_{\triangle AEC}= 6$,求$AB$的长。
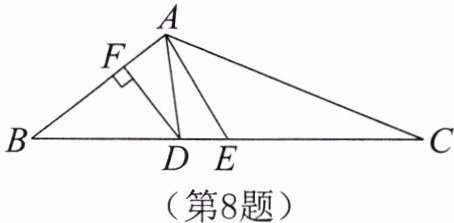

答案:
5。
1. 下列命题是真命题的是( )
A.若$ab= 0$,则$a= 0$
B.相等的角是对顶角
C.若$|a|<b$,则$a^2<b^2$
D.同旁内角互补
A.若$ab= 0$,则$a= 0$
B.相等的角是对顶角
C.若$|a|<b$,则$a^2<b^2$
D.同旁内角互补
答案:
C
2. 如图,在$\triangle ABC$中,$AB= 2AC$,$AD平分\angle BAC$,延长$AD至点E$,使$DE= AD$,连结$BE$。若$S_{\triangle BDE}= 12$,则$S_{\triangle ABC}$为( )
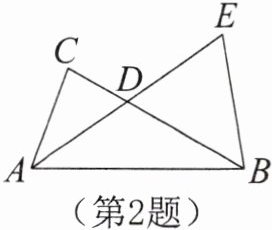
A.12
B.16
C.18
D.20

A.12
B.16
C.18
D.20
答案:
C
3. 如图,$\triangle EFG的三个顶点E$,$G和F分别在平行线AB$,$CD$上,$FH平分\angle EFG$,交线段$EG于点H$,若$\angle AEF= 36^\circ$,$\angle BEG= 57^\circ$,则$\angle EHF$的大小为 。
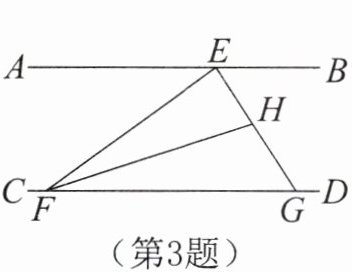

答案:
75°。
4. 如图,已知$\angle A= 60^\circ$,$\angle B= 40^\circ$,$\angle C= 30^\circ$,则$\angle D+\angle E= $ 。
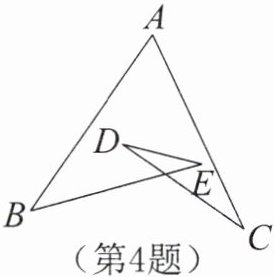

答案:
50°。
5. 如图所示,在$\triangle ABC$中,$\angle A= 30^\circ$,$\angle ABC= 70^\circ$,$\triangle ABC的外角\angle BCD的平分线CE交AB的延长线于点E$。
(1)求$\angle BCE$的度数;
(2)过点$D作DF // CE$,交$AB的延长线于点F$,求$\angle F$的度数。
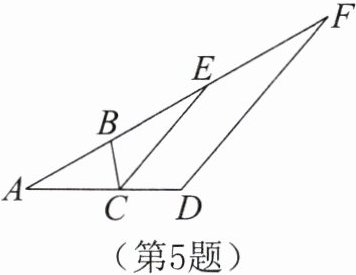
(1)求$\angle BCE$的度数;
(2)过点$D作DF // CE$,交$AB的延长线于点F$,求$\angle F$的度数。

答案:
(1)50°;
(2)20°。
(1)50°;
(2)20°。
查看更多完整答案,请扫码查看


