《2025年课前课后快速检测八年级数学上册浙教版》

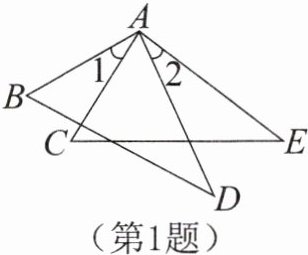
1. 如图,已知$AB= AC$,$AD= AE$。若要根据SAS判定$\triangle ABD \cong \triangle ACE$,则需要添加的条件是( )

A.$\angle B= \angle C$
B.$\angle D= \angle E$
C.$\angle 1= \angle 2$
D.$\angle B= \angle E$
]

答案： C

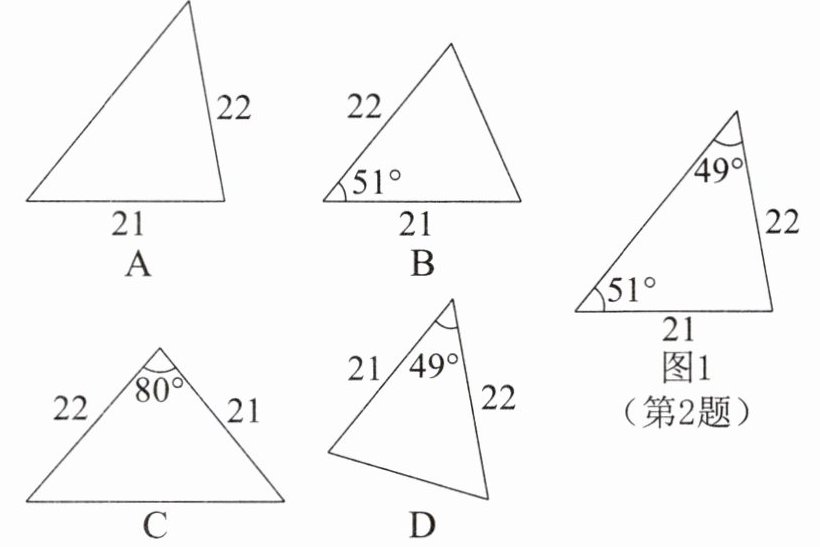
2. 下列三角形与图1全等的三角形是( )



A.
B.
C.
D.

答案： C

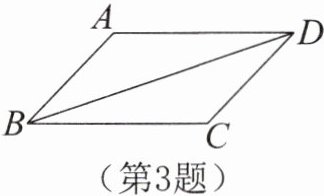
3. 如图,$\angle ABD= \angle CDB$,$AB= 2$,$AD= 4$,要使$\triangle ABD \cong \triangle CDB$,添加下列条件正确的是( )

A.$BC= 2$
B.$BC= 4$
C.$CD= 2$
D.$CD= 4$
]

答案： C

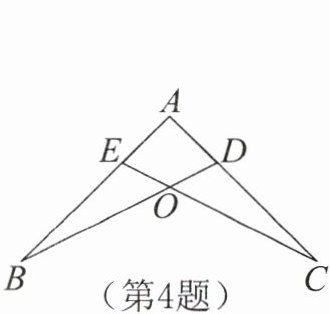
4. 如图,$AB= AC$,$AD= AE$,请写出图中全等的三角形______。(写出一组即可)
]

答案： △ABD≌△ACE(答案不唯一)。

5. 如图,线段$AB与CF交于点E$,$D为CF$上一点,连结$AD$,$AF$,$BC$,已知$AD= BC$,$\angle 1= \angle 2$。根据SAS判定$\triangle ADF和\triangle BCE$全等,还需具备的条件是______。(填一个即可)
]

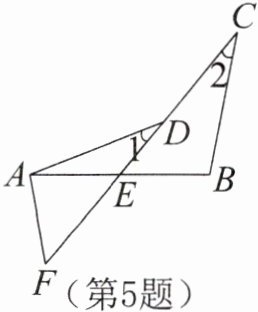
答案： DF=CE (答案不唯一)。

6. 如图,点$C在线段BD$上,点$A$,$E在BD$的同一侧,$AB \perp BD于点B$,$ED \perp BD于点D$,且$AB= CD$,$BC= DE$,那么$\angle ACE= $______°。
]

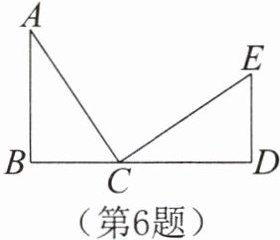
答案： 90。

7. 如图,小明家有一个玻璃容器,他想测量一下它的内径是多少？但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条$AB$,$CD$的中点连在一起,木条可以绕中点$O$自由转动,这样只要测量点$A$,$C$的距离,就可以知道玻璃容器的内径,你知道其中的道理吗？请说明理由。
]

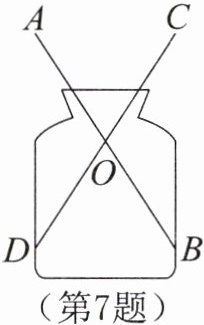
答案： 【解析】：本题可根据全等三角形的判定定理和性质来证明测量$AC$的距离就可以知道玻璃容器的内径$BD$的长度。
已知两根小木条$AB$，$CD$的中点连在一起为点$O$，且木条可绕中点$O$自由转动，所以$OA = OB$，$OC = OD$。
在$\triangle AOC$和$\triangle BOD$中，$OA = OB$，$\angle AOC = \angle BOD$（对顶角相等），$OC = OD$。
根据全等三角形的判定定理“边角边”（$SAS$），可以得出$\triangle AOC\cong\triangle BOD$。
再根据全等三角形的性质：全等三角形的对应边相等，可知$AC = BD$。
所以只要测量点$A$，$C$的距离，就可以知道玻璃容器的内径$BD$的长度。
【答案】：证明：
连接$AC$，$BD$。
因为点$O$是$AB$，$CD$的中点，
所以$OA = OB$，$OC = OD$。
在$\triangle AOC$和$\triangle BOD$中，
$\begin{cases}OA = OB\\\angle AOC = \angle BOD\\OC = OD\end{cases}$
所以$\triangle AOC\cong\triangle BOD(SAS)$。
所以$AC = BD$。
故只要测量点$A$，$C$的距离，就可以知道玻璃容器的内径。

8. 如图,点$D$,$E在\triangle ABC的边BC$上,且$BE= CD$,$AD= AE$,$\angle 1= \angle 2= 110^\circ$,求证：$\triangle ADB \cong \triangle AEC$。
]

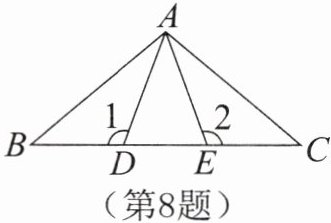
答案： 证明：
∵∠1=∠2=110°，
∴∠ADB=180°-∠1=70°，∠AEC=180°-∠2=70°，
∴∠ADB=∠AEC。
∵BE=CD，
∴BE-DE=CD-DE，即BD=CE。
在△ADB和△AEC中，
∵∠ADB=∠AEC，AD=AE，BD=CE，
∴△ADB≌△AEC（SAS）。