《2025年课前课后快速检测八年级数学上册浙教版》

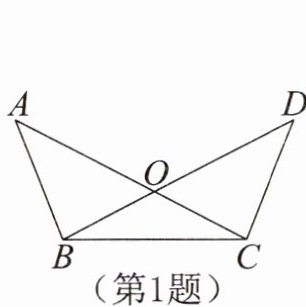
1.如图,AC,BD相交于点O,∠A= ∠D,如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是( )

A.OA= OD
B.AB= CD
C.∠ABO= ∠DCO
D.∠ABC= ∠DCB

答案： C

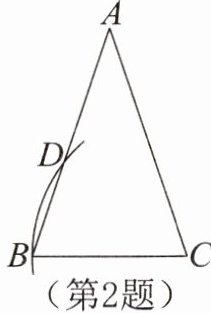
2.如图,在△ABC中,AB= AC,∠BAC= 36°,以C为圆心,CB长为半径画弧,交AB于点B和点D。若BC= a,BD= b,则△ADC的周长是 ( )

A.2a+2b
B.3a+b
C.3a
D.3a+2b

答案： B

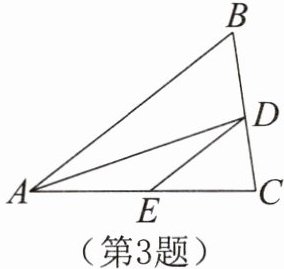
3.如图所示,在△ABC中,AD是∠BAC的平分线,DE//AB交AC于点E,若DE= 6,CE= 5,则AC的长为 。

答案： 11

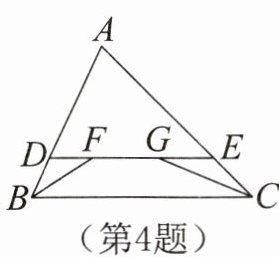
4.如图,在△ABC中,ED//BC,∠ABC和∠ACB的平分线分别交ED于点F,G,若FG= 2,ED= 6,则DB+EC的值为 。

答案： 4

5.如图,△ABC是等边三角形,D,E,F分别是AC,AB,BC上的点,且AD= BE= CF。求证：△DEF是等边三角形。

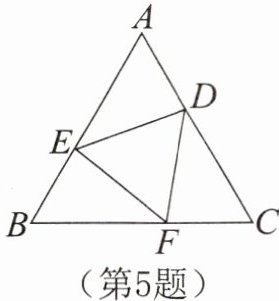
答案： 【解析】：本题可根据等边三角形的性质得出三边相等、三角相等，再结合已知条件$AD = BE = CF$，通过证明三角形全等得出对应边相等，进而证明$\triangle DEF$是等边三角形。
【答案】：
证明：
∵$\triangle ABC$是等边三角形，
∴$AB = BC = AC$，$\angle A=\angle B=\angle C = 60^{\circ}$。
∵$AD = BE = CF$，
∴$AB - BE = BC - CF = AC - AD$，即$AE = BF = CD$。
在$\triangle ADE$、$\triangle BEF$和$\triangle CFD$中，
$\begin{cases}AD = BE = CF\\\angle A=\angle B=\angle C\\AE = BF = CD\end{cases}$
∴$\triangle ADE\cong\triangle BEF\cong\triangle CFD(SAS)$。
∴$DE = EF = FD$。
∴$\triangle DEF$是等边三角形。

6.如图,CE平分∠ACB且CE⊥DB于点E,∠DAB= ∠DBA,若AC= 14,△CDB的周长为20,求DB的长。

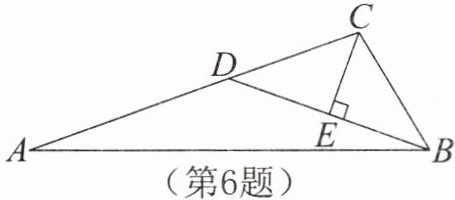
答案： 8

1.如图,已知P是射线ON上一动点(即点P可在射线ON上运动),∠O= 30°,当∠A= 时,△AOP为等腰三角形。

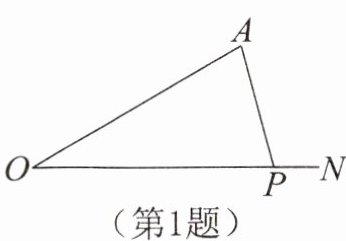
答案： 75°或120°或30°

2.如图所示,在△ABC中,∠ABC= 2∠ACB,AE为高线,若BE= 1,AB= 4,则BC= 。

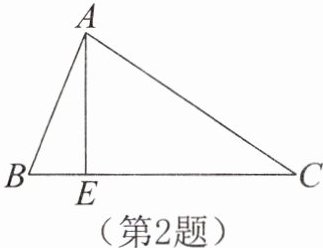
答案： 6