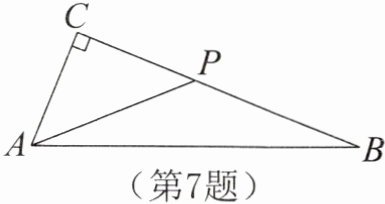
7. 如图,在Rt△ABC中,∠C= 90°。在边BC上有一点P,连结AP,且PA= PB,若AC= 2,CB= 5,求PA的长。

答案:
$\frac{29}{10}$
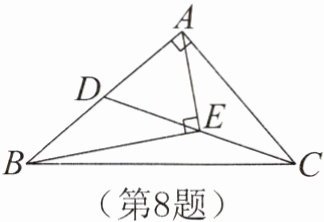
8. 如图,在Rt△ABC中,∠BAC= 90°,AB= 4,CD是△ABC的中线,E是CD的中点,连结AE,BE,若AE⊥BE,垂足为E,求$AC^2$的值。

答案:
12
1. 一直角三角形的一条直角边长是7cm,另一条直角边与斜边长的和是49cm,则斜边的长为( )
A.18cm
B.20cm
C.24cm
D.25cm
A.18cm
B.20cm
C.24cm
D.25cm
答案:
D
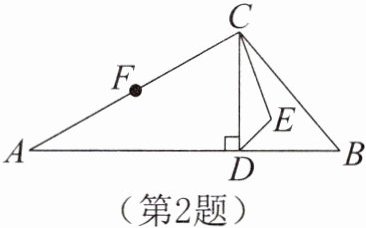
2. 如图,在△ABC中,∠B= 50°,CD⊥AB于点D,∠BCD和∠BDC的角平分线相交于点E,F为边AC的中点,CD= CF,则∠ACD+∠CED= ( )
A.125°
B.145°
C.175°
D.190°

A.125°
B.145°
C.175°
D.190°
答案:
C
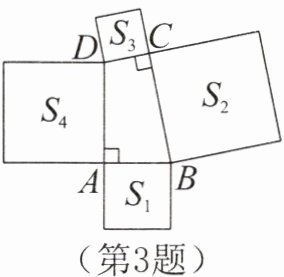
3. 如图所示,在四边形ABCD中,∠DAB= ∠BCD= 90°,分别以四边形的四条边为边向外作四个正方形,它们的面积分别是$S_1,S_2,S_3,S_4$。若$S_1+S_4= 100$,$S_3= 36$,则$S_2$的值是______。

答案:
64
4. 如图,在等边△ABC中,BC= 2,D是AB的中点,过点D作DF⊥AC于点F,过点F作EF⊥BC于点E,则BE的长是______。
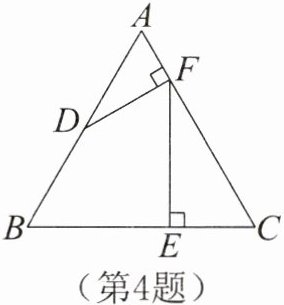

答案:
$\frac{5}{4}$
5. 如图,在Rt△ABC中,CD是斜边AB上的高,CE是AB上的中线,CF是∠BCA的平分线。求证:∠1= ∠2。
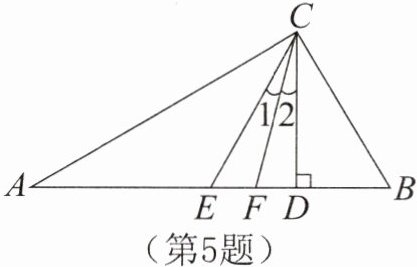

答案:
【解析】:本题可根据直角三角形的性质、三角形中位线的性质以及角平分线的性质来证明$\angle1 = \angle2$。
步骤一:根据直角三角形斜边中线的性质得到$CE = AE$,进而推出$\angle EAC=\angle ECA$。
在$Rt\triangle ABC$中,$CE$是斜边$AB$上的中线,根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,可得$CE = AE=\frac{1}{2}AB$。
因为$CE = AE$,所以$\triangle ACE$是等腰三角形,根据等腰三角形的性质:等腰三角形的两个底角相等,可得$\angle EAC=\angle ECA$。
步骤二:根据$CD\perp AB$得到$\angle ADC = 90^{\circ}$,进而推出$\angle ACD+\angle EAC = 90^{\circ}$。
已知$CD$是斜边$AB$上的高,所以$\angle ADC = 90^{\circ}$。
在$Rt\triangle ACD$中,根据直角三角形两锐角互余,可得$\angle ACD+\angle CAD = 90^{\circ}$,即$\angle ACD+\angle EAC = 90^{\circ}$。
步骤三:根据$\angle ACB = 90^{\circ}$得到$\angle ECA+\angle ECB = 90^{\circ}$,进而推出$\angle ACD=\angle ECB$。
因为$\angle ACB = 90^{\circ}$,即$\angle ECA+\angle ECB = 90^{\circ}$,又因为$\angle ACD+\angle EAC = 90^{\circ}$且$\angle EAC=\angle ECA$,所以$\angle ACD=\angle ECB$。
步骤四:根据角平分线的性质得到$\angle ACF=\angle ECF$。
已知$CF$是$\angle BCA$的平分线,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线,可得$\angle ACF=\angle ECF$。
步骤五:通过角的运算证明$\angle1 = \angle2$。
因为$\angle1=\angle ACF - \angle ACD$,$\angle2=\angle ECF - \angle ECB$,又因为$\angle ACF=\angle ECF$,$\angle ACD=\angle ECB$,所以$\angle1 = \angle2$。
【答案】:证明:
∵$CE$是$Rt\triangle ABC$斜边$AB$上的中线,
∴$CE = AE=\frac{1}{2}AB$,
∴$\angle EAC=\angle ECA$。
∵$CD\perp AB$,
∴$\angle ADC = 90^{\circ}$,
∴$\angle ACD+\angle CAD = 90^{\circ}$,即$\angle ACD+\angle EAC = 90^{\circ}$。
∵$\angle ACB = 90^{\circ}$,
∴$\angle ECA+\angle ECB = 90^{\circ}$,
∴$\angle ACD=\angle ECB$。
∵$CF$是$\angle BCA$的平分线,
∴$\angle ACF=\angle ECF$。
∵$\angle1=\angle ACF - \angle ACD$,$\angle2=\angle ECF - \angle ECB$,
∴$\angle1 = \angle2$。
步骤一:根据直角三角形斜边中线的性质得到$CE = AE$,进而推出$\angle EAC=\angle ECA$。
在$Rt\triangle ABC$中,$CE$是斜边$AB$上的中线,根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,可得$CE = AE=\frac{1}{2}AB$。
因为$CE = AE$,所以$\triangle ACE$是等腰三角形,根据等腰三角形的性质:等腰三角形的两个底角相等,可得$\angle EAC=\angle ECA$。
步骤二:根据$CD\perp AB$得到$\angle ADC = 90^{\circ}$,进而推出$\angle ACD+\angle EAC = 90^{\circ}$。
已知$CD$是斜边$AB$上的高,所以$\angle ADC = 90^{\circ}$。
在$Rt\triangle ACD$中,根据直角三角形两锐角互余,可得$\angle ACD+\angle CAD = 90^{\circ}$,即$\angle ACD+\angle EAC = 90^{\circ}$。
步骤三:根据$\angle ACB = 90^{\circ}$得到$\angle ECA+\angle ECB = 90^{\circ}$,进而推出$\angle ACD=\angle ECB$。
因为$\angle ACB = 90^{\circ}$,即$\angle ECA+\angle ECB = 90^{\circ}$,又因为$\angle ACD+\angle EAC = 90^{\circ}$且$\angle EAC=\angle ECA$,所以$\angle ACD=\angle ECB$。
步骤四:根据角平分线的性质得到$\angle ACF=\angle ECF$。
已知$CF$是$\angle BCA$的平分线,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线,可得$\angle ACF=\angle ECF$。
步骤五:通过角的运算证明$\angle1 = \angle2$。
因为$\angle1=\angle ACF - \angle ACD$,$\angle2=\angle ECF - \angle ECB$,又因为$\angle ACF=\angle ECF$,$\angle ACD=\angle ECB$,所以$\angle1 = \angle2$。
【答案】:证明:
∵$CE$是$Rt\triangle ABC$斜边$AB$上的中线,
∴$CE = AE=\frac{1}{2}AB$,
∴$\angle EAC=\angle ECA$。
∵$CD\perp AB$,
∴$\angle ADC = 90^{\circ}$,
∴$\angle ACD+\angle CAD = 90^{\circ}$,即$\angle ACD+\angle EAC = 90^{\circ}$。
∵$\angle ACB = 90^{\circ}$,
∴$\angle ECA+\angle ECB = 90^{\circ}$,
∴$\angle ACD=\angle ECB$。
∵$CF$是$\angle BCA$的平分线,
∴$\angle ACF=\angle ECF$。
∵$\angle1=\angle ACF - \angle ACD$,$\angle2=\angle ECF - \angle ECB$,
∴$\angle1 = \angle2$。
查看更多完整答案,请扫码查看


