《2025年课前课后快速检测八年级数学上册浙教版》

3.如图所示,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D。若∠BOD= 46°,∠C= 20°,则∠ADC= ______°。

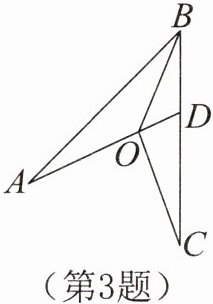
答案： 72。

4.如图,点D在△ABC的边AC上,将△ABD沿直线BD折叠,点A正好落在边BC上的点P处。若△ABC的面积为80,△DBC的面积为50,则$\frac{BP}{PC}= $______。

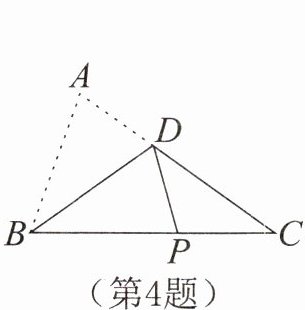
答案： $\frac{3}{2}$。

5.如图,将已知四边形分别在格点图中补成关于已知直线l,m,n,p为对称轴的轴对称图形。

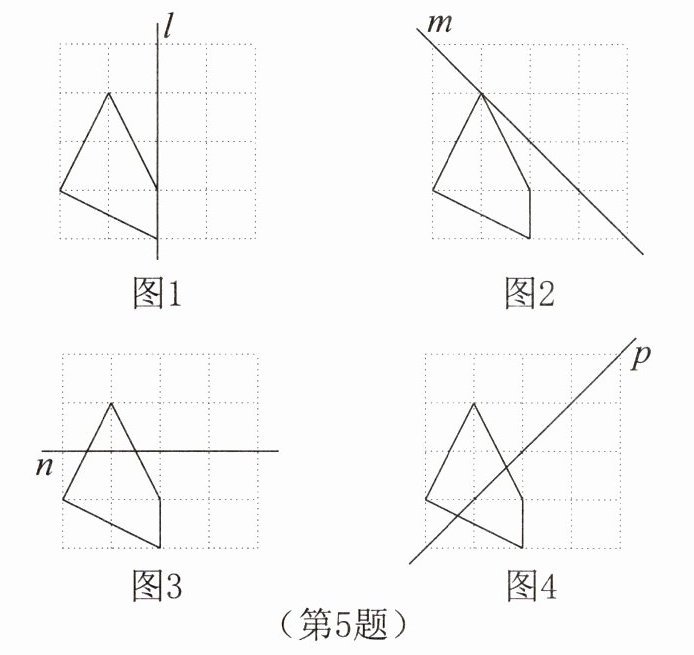
答案： 【解析】：
题目考查了轴对称图形的绘制，需要利用轴对称的性质，即关于对称轴对称的点，其到对称轴的距离相等且连线垂直于对称轴，来补全四边形关于各条直线的轴对称图形。
【答案】：
图略（按照轴对称的性质，分别找出四边形各顶点关于直线$l$、$m$、$n$、$p$的对称点，然后依次连接这些对称点，即可得到关于各条直线的轴对称图形）。

6.如图,在四边形ABCD中,∠A= 100°,∠C= 70°,点M,N分别在AB,BC上,将△BMN沿直线MN翻折,得到△FMN。若MF//AD,FN//DC,求∠B的度数。

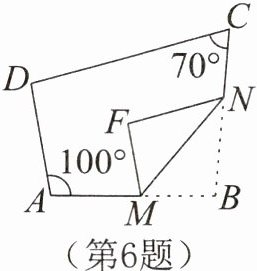
答案： $95^\circ$。

1.如图,在△ABC中,D为BC边上任意一点(不与点B,C重合),连结AD,分别作点D关于AB,AC的对称点E,F,分别连结AE,AF,若∠EAF= 130°,∠C= 45°,则∠B的度数为______。

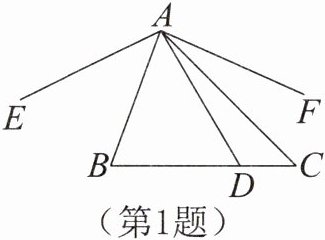
答案： $70^\circ$。

2.如图所示,将长方形纸片ABCD沿MN和PQ折叠得到一个轴对称的帽子,折痕角∠AMN= ∠DPQ,点A,D的对应点分别为G,H,折叠后点B,C的对应点恰好都在E,若折痕角∠AMN= 110°,求帽子顶角∠NEQ的度数。

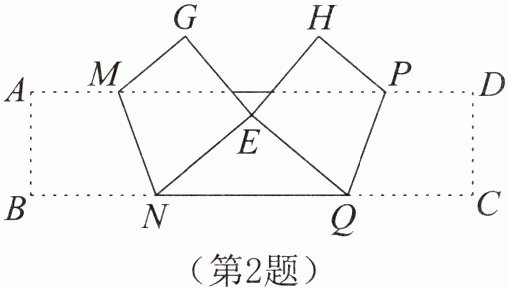
答案： $100^\circ$。