第65页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 观察下面的图形,你能把它们分成两类吗?(填序号)分类的依据是什么?
第一类:( ),依据是( ),叫作( )形。
第一类:( ),依据是( ),叫作( )形。

第一类:( ),依据是( ),叫作( )形。
第一类:( ),依据是( ),叫作( )形。

答案:
第一类:(①⑤),依据是(两组对边分别平行),叫作(平行四边)形。
第二类:(②③④),依据是(只有一组对边平行),叫作(梯)形。
第二类:(②③④),依据是(只有一组对边平行),叫作(梯)形。
2. 比较上题中的图②③④,它们的相同点是( ),平行的一组对边分别叫作( )和( ),不平行的一组对边叫作( );不同点是图③中有一个角是直角,所以又叫作( )梯形,图②的两( )相等,又叫作( )梯形。
答案:
解析:本题考查梯形,等腰梯形和直角梯形的性质。
答案:都有一组对边平行;上底;下底;腰;直角;腰;等腰。
答案:都有一组对边平行;上底;下底;腰;直角;腰;等腰。
1. 选择。
如右下图,一个四边形被挡住了一部分,这个四边形( )。
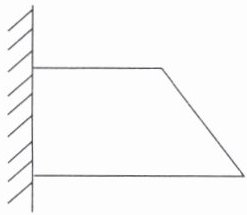
A.一定是平行四边形
B.一定是梯形
C.一定是直角梯形
D.可能是平行四边形,也可能是梯形
如右下图,一个四边形被挡住了一部分,这个四边形( )。

A.一定是平行四边形
B.一定是梯形
C.一定是直角梯形
D.可能是平行四边形,也可能是梯形
答案:
解析:本题考查平行四边形和梯形的定义。
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。
梯形的定义:只有一组对边平行的四边形叫做梯形。
从图中可以看到,这个四边形有一组对边看起来是平行的,但另一组对边被挡住了,无法确定是否平行。
如果另一组对边也平行,那么这个四边形就是平行四边形;
如果另一组对边不平行,那么这个四边形就是梯形。
所以,这个四边形可能是平行四边形,也可能是梯形。
答案:D。
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。
梯形的定义:只有一组对边平行的四边形叫做梯形。
从图中可以看到,这个四边形有一组对边看起来是平行的,但另一组对边被挡住了,无法确定是否平行。
如果另一组对边也平行,那么这个四边形就是平行四边形;
如果另一组对边不平行,那么这个四边形就是梯形。
所以,这个四边形可能是平行四边形,也可能是梯形。
答案:D。
2. 下图中有( )个平行四边形、( )个梯形。最大的梯形ABCD的四个角的度数之和是( )度。
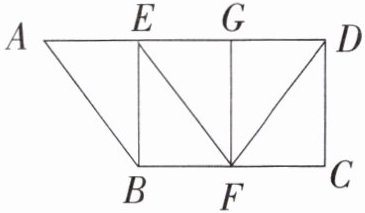

答案:
3;6;360
查看更多完整答案,请扫码查看


