《2025年预学与导学四年级数学上册人教版》

1. 填空。
(1)直角= ( )度 平角= ( )度 周角= ( )度
(2)1周角= ( )平角= ( )直角 1平角= ( )直角

答案： 解析：
(1) 题目考查的是角的基本分类和定义，特别是直角、平角、周角的度数。
直角是角度为90度的角，平角是角度为180度的角，周角是角度为360度的角。
(2) 题目考查的是周角、平角和直角之间的关系。
1周角等于360度，所以等于2个平角（每个平角180度），也等于4个直角（每个直角90度）。
1平角等于180度，所以等于2个直角。
答案：
(1) 直角= 90度，平角= 180度，周角= 360度
(2) 1周角= 2平角= 4直角，1平角= 2直角

2. 判断下面各题,对的画“√”,错的画“×”。
(1)平角是一条直线,周角是一条射线。………………( )
(2)小于90度的角叫作锐角,大于90度的角叫作钝角。( )
(3)两个锐角的度数之和一定比一个直角的度数大。……( )

答案： 解析：本题考查角的分类及定义。
(1) 平角是角度为180度的角，它仍然是一个角，由一个顶点和两条射线组成，不是一条直线。周角是角度为360度的角，它也是一个角，由一个顶点和两条重合的射线组成，在画出时看起来像一条射线，但实际上它表示的是一个完整的圆周角度，因此它也不是一条射线。所以此题错误。
(2) 锐角是小于90度的角，这是正确的。但是钝角的定义是大于90度且小于180度的角，题目中只提到了大于90度，没有提到小于180度，所以此题错误。
(3) 锐角是小于90度的角，所以两个锐角的和可能小于90度（如30度和40度），也可能等于90度（如45度和45度），或者大于90度但小于180度（如60度和70度）。所以两个锐角的度数之和并不一定比一个直角的度数大。此题错误。
答案：
(1)×
(2)×
(3)×

3. 选择。
(1)把平角分成两个角,其中一个是钝角,则另一个肯定是( )。
A. 锐角 B. 直角 C. 钝角
(2)比90°大但比180°小的角一定是( )。
A. 锐角 B. 直角 C. 钝角
(3)钟面上,上午9时整,时针与分针组成的角是( )。
A. 锐角 B. 直角 C. 钝角

答案： 解析：
(1) 平角是180°。钝角是大于90°但小于180°的角。如果一个平角被分成一个钝角和一个其他角，那么其他角必定小于90°，因此是锐角。
(2) 比90°大但比180°小的角，根据角的定义，这样的角是钝角。
(3) 钟面上，上午9时整时，时针指向9，分针指向12。一个小时对应的角度是30°（因为360°/12小时 = 30°/小时），所以9时整时，时针与分针之间相隔3个小时的距离，即90°，这是直角。
答案：
(1) A. 锐角
(2) C. 钝角
(3) B. 直角

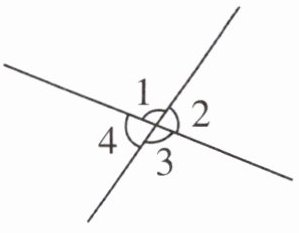
4. 如右图,已知$\angle 1= 98^\circ,求\angle 2,\angle 3,\angle 4$的度数。

答案： 解析：本题可根据平角的度数以及角之间的关系来求解$\angle 2$、$\angle 3$、$\angle 4$的度数。
步骤一：求$\angle 2$的度数
观察图形可知，$\angle 1$与$\angle 2$组成一个平角，因为平角的度数是$180^{\circ}$，所以$\angle 1 + \angle 2 = 180^{\circ}$。
已知$\angle 1 = 98^{\circ}$，将其代入上式可得：
$\angle 2 = 180^{\circ} - \angle 1 = 180^{\circ} - 98^{\circ} = 82^{\circ}$
步骤二：求$\angle 3$的度数
由图可知，$\angle 2$与$\angle 3$也组成一个平角，即$\angle 2 + \angle 3 = 180^{\circ}$。
已经求得$\angle 2 = 82^{\circ}$，将其代入上式可得：
$\angle 3 = 180^{\circ} - \angle 2 = 180^{\circ} - 82^{\circ} = 98^{\circ}$
步骤三：求$\angle 4$的度数
同样，$\angle 1$与$\angle 4$组成一个平角，即$\angle 1 + \angle 4 = 180^{\circ}$。
已知$\angle 1 = 98^{\circ}$，将其代入上式可得：
$\angle 4 = 180^{\circ} - \angle 1 = 180^{\circ} - 98^{\circ} = 82^{\circ}$
答案：$\angle 2 = 82^{\circ}$，$\angle 3 = 98^{\circ}$，$\angle 4 = 82^{\circ}$。

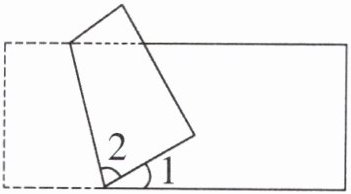
右面是一张长方形纸折叠后形成的图形。已知$\angle 1= 30^\circ,则\angle 2$是多少度？

答案： 解：
因为长方形纸折叠，所以$\angle 2 = \angle 3$（折叠性质），又因为$\angle 1+\angle 2+\angle 3 = 180^{\circ}$（平角定义），且$\angle 1 = 30^{\circ}$，即$30^{\circ}+2\angle 2 = 180^{\circ}$，移项可得$2\angle 2=180^{\circ}- 30^{\circ}=150^{\circ}$，两边同时除以$2$，$\angle 2 = 150^{\circ}÷2 = 75^{\circ}$。
所以$\angle 2$是$75^{\circ}$。