《2025年一本计算题满分训练七年级数学全一册人教版》

1.【一题多解】$(-1)+(-2)+(+3)+(+4)+(-5)+(-6)+(+7)+(+8)+... +(+199)+(+200).$

答案： 一题多解 解:方法1:分组求和法
原式=[(-1)+(-2)+(+3)+(+4)]+[(-5)+(-6)+(+7)+(+8)]+…+[(-197)+(-198)+(+199)+(+200)]=$\underset{50个}{\underbrace{4+4+\cdots +4}}$=200.
方法2：
原式=[(-1)+(+3)]+[(-2)+(+4)]+…+[(-198)+(+200)]=$\underset{100个}{\underbrace{2+2+\cdots +2}}$=200.

2.【易错】$(-2021\frac {5}{6})+(-2022\frac {2}{3})+(-1\frac {1}{2})+4042\frac {3}{4}.$

答案： 方法:拆分法
解:原式=$[(-2021)+(-\frac{5}{6})]+[(-2022)+(-\frac{2}{3})]+[(-1)+(-\frac{1}{2})]+(4042+\frac{3}{4})$=[(-2021)+(-2022)+(-1)+4042]+$[(-\frac{5}{6})+(-\frac{2}{3})+(-\frac{1}{2})+\frac{3}{4}]$=-2-$\frac{5}{4}$=$-3\frac{1}{4}$.

3.$(-1)+2+(-3)+4+(-5)+6+... +(-2023)+2024+(-2025).$

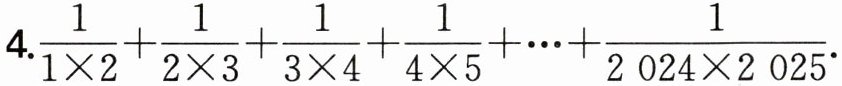
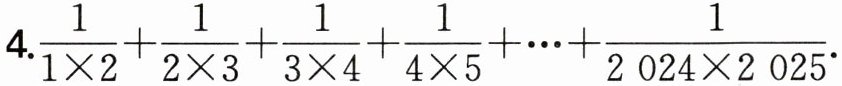
答案： 解:原式=[(-1)+2]+[(-3)+4]+[(-5)+6]+…+[(-2023)+2024]+(-2025)=$\underset{1012个}{\underbrace{1+1+1+\cdots +1}}$+(-2025)=1012+(-2025)=-1013.

5.【一题多解】$\frac {1}{2}+\frac {1}{4}+\frac {1}{8}+\frac {1}{16}+\frac {1}{32}+\frac {1}{64}+\frac {1}{128}+\frac {1}{256}.$

答案：
一题多解 解:方法1:错位相减法
设$S=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256}$.①
两边同时乘2,得$2S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}$.②
②-①,得$S=1-\frac{1}{256}=\frac{255}{256}$.
视频辅导
方法2:拆分法
原式=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}+\cdots +\frac{1}{128}-\frac{1}{256}=1-\frac{1}{256}=\frac{255}{256}$.
方法3:数形结合法
如图,在面积为“1”的正方形中,易得$\frac{1}{2}+\frac{1}{4}=1-\frac{1}{4}=\frac{3}{4}$,$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=1-\frac{1}{8}=\frac{7}{8}$,...

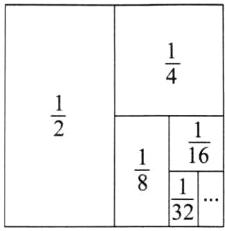
∴原式=$1-\frac{1}{256}=\frac{255}{256}$.