《2025年一本计算题满分训练七年级数学全一册人教版》

1.某校组织学生参加文艺汇演,若单租45座客车若干辆,则刚好坐满;若单租60座客车,则可少租一辆,且余15个座位.(客车座位数为乘客座位数)
(1)【一题多解】求参加文艺汇演的总人数;
(2)已知一辆45座客车每天的租金为250元,一辆60座客车每天的租金为300元,问:单租哪种客车更省钱?

答案： $(1)$ 求参加文艺汇演的总人数
方法一：列方程求解
设单租$45$座客车$x$辆，则参加文艺汇演的总人数为$45x$人。
根据单租$60$座客车的情况可列方程：
$45x = 60(x - 1)-15$
解这个方程：
$\begin{aligned}45x&=60x - 60 - 15\\60x - 45x&=60 + 15\\15x&=75\\x&=5\end{aligned}$
则总人数为$45×5 = 225$（人）
方法二：算术方法求解
单租$60$座客车比单租$45$座客车少租一辆，且$60$座客车坐满的话比$45$座客车坐满的人数多$60 + 15=75$人。
每辆$60$座客车比$45$座客车多$60 - 45 = 15$个座位。
所以$45$座客车的辆数为$75÷15 = 5$辆。
则总人数为$45×5 = 225$人。
$(2)$ 比较哪种客车更省钱
- 若单租$45$座客车：
需要$5$辆，租金为$250×5 = 1250$元。
- 若单租$60$座客车：
总人数$225$人，$225÷60 = 3$（辆）$\cdots\cdots45$（人），所以需要$4$辆，租金为$300×4 = 1200$元。
因为$1200\lt1250$，所以单租$60$座客车更省钱。
综上，$(1)$参加文艺汇演的总人数为$\boldsymbol{225}$人；$(2)$单租$\boldsymbol{60}$座客车更省钱。

2.从甲地到乙地,驾驶长途汽车原来需要8h,开通高速公路后,路程缩短了40km,平均车速增加了30km/h,现在只需要4.5h即可到达,求长途汽车原来行驶的平均速度.

答案： 50 km/h

3.一个由6个正方形组成的长方形如图所示,已知中间最小的一个正方形的边长为2,求这个长方形的面积.

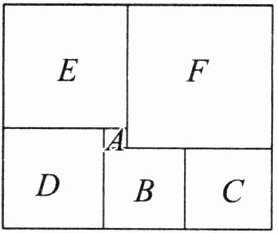
答案： 1. 设正方形$B$的边长为$x$：
则正方形$D$的边长为$x + 2$，正方形$E$的边长为$x+2 + 2=x + 4$，正方形$F$的边长为$x+4 + 2=x + 6$，正方形$C$的边长为$x$。
2. 根据长方形的长相等列方程：
由长方形的长$L=(x + 2)+(x+4)=(x + 6)+x$（这里也可以根据长方形长的另一种表示方法$(x + 2)+x+(x)=(x + 4)+(x + 6)$）。
先看$(x + 2)+(x+4)=(x + 6)+x$，左边$=x + 2+x + 4=2x+6$，右边$=x + 6+x=2x+6$（恒成立）；再看$(x + 2)+x+(x)=(x + 4)+(x + 6)$。
解$(x + 2)+x+(x)=(x + 4)+(x + 6)$：
左边$=x + 2+x+x=3x + 2$，右边$=x + 4+x + 6=2x+10$。
移项可得$3x+2-(2x + 10)=0$，即$3x+2 - 2x-10 = 0$。
合并同类项得$(3x-2x)+(2 - 10)=0$，也就是$x-8 = 0$，解得$x = 8$。
3. 求长方形的长和宽：
长方形的长$l=(x + 2)+(x+4)=(8 + 2)+(8 + 4)=10 + 12=22$。
长方形的宽$w=(x + 4)+x=(8 + 4)+8=20$。
4. 求长方形的面积$S$：
根据长方形面积公式$S = l× w$，这里$l = 22$，$w = 20$，所以$S=22×20 = 440$。
所以这个长方形的面积是$440$。

4.如图,点A,B分别位于数轴上原点O的两侧,$AB= 12$,且$OA= 2OB$.动点P从点A出发以每秒3个单位长度的速度向右运动,同时动点Q从点B出发以每秒1个单位长度的速度向左运动.
(1)求数轴上点A,B对应的数各是多少;
(2)当$OP= OQ$时,求运动的时间.

答案： 1. （1）
设$OB = x$，因为$OA = 2OB$，所以$OA = 2x$。
又因为$AB=OA + OB$，且$AB = 12$，所以$2x + x=12$。
合并同类项得$3x = 12$，解得$x = 4$。
因为点$A$在原点左侧，点$B$在原点右侧，所以点$A$对应的数是$-8$，点$B$对应的数是$4$。
2. （2）
设运动时间为$t$秒。
点$P$从点$A(-8)$出发，速度是每秒$3$个单位长度，向右运动$t$秒后，点$P$表示的数为$-8 + 3t$；点$Q$从点$B(4)$出发，速度是每秒$1$个单位长度，向左运动$t$秒后，点$Q$表示的数为$4−t$。
当$OP = OQ$时，分两种情况：
情况一：$-8 + 3t=-(4 - t)$。
去括号得$-8 + 3t=-4 + t$。
移项得$3t - t=-4 + 8$。
合并同类项得$2t = 4$，解得$t = 2$。
情况二：$-8 + 3t=4 - t$。
移项得$3t + t=4 + 8$。
合并同类项得$4t = 12$，解得$t = 3$。
综上，（1）点$A$对应的数是$-8$，点$B$对应的数是$4$；（2）运动时间为$2$秒或$3$秒。