第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
7. (2024·扬州仪征期末)如图所示是用水下照相机拍摄的小球在水中下落的一张频闪照片,已知水池壁上每块瓷砖高度均为12 cm,闪光灯每隔0.2s时间闪亮一次(即拍摄一次).已知小球从B位置开始匀速运动,则小球从A位置到D位置过程中的平均速度为
0.8
m/s,小球通过C点时的速度为0.6
m/s.
答案:
0.8 0.6 [解析]小球从 A 位置到 D 位置的平均速度$v=\frac {s}{t}=\frac {4×0.12m}{3×0.2s}=0.8m/s$.匀速运动速度不变,小球通过 C 点时的速度等于 BD 段的速度$v'=\frac {s'}{t'}=\frac {2×0.12m}{2×0.2s}=0.6m/s.$
8. (2024·宿迁泗洪县期末)如图甲所示,灰色部分的“面积”在数值上等于物体在2s经过的路程.从v-t图像可看出速度图线和时间横轴所夹的“面积”可以表示该时间内通过的路程,我们能利用这一点很方便地计算出路程.小明同学在笔直的跑道上跑步,他在跑步过程中的速度与时间图像如图乙所示,则在0~60s内他通过的路程是
100
m,在0~80s内的平均速度为1.5
m/s.
答案:
100 1.5 [解析]由图像可知,0~20 s 小明做加速运动,通过的路程$s_{1}=v_{1}t_{1}=\frac {1}{2}×2m/s×20s=20m$;20~60 s 小明做匀速运动,通过的路程$s_{2}=v_{2}t_{2}=40s×2m/s=80m$;60~80 s 小明做减速运动,通过的路程$s_{3}=v_{3}t_{3}=\frac {1}{2}×2m/s×20s=20m$.在 0~60 s 内小明通过的路程$s_{0}=s_{1}+s_{2}=20m+80m=100m$;在 0~80 s 时间内的总路程$s=s_{1}+s_{2}+s_{3}=20m+80m+20m=120m$,在 0~80 s 时间内平均速度$v=\frac {s}{t}=\frac {120m}{80s}=1.5m/s.$
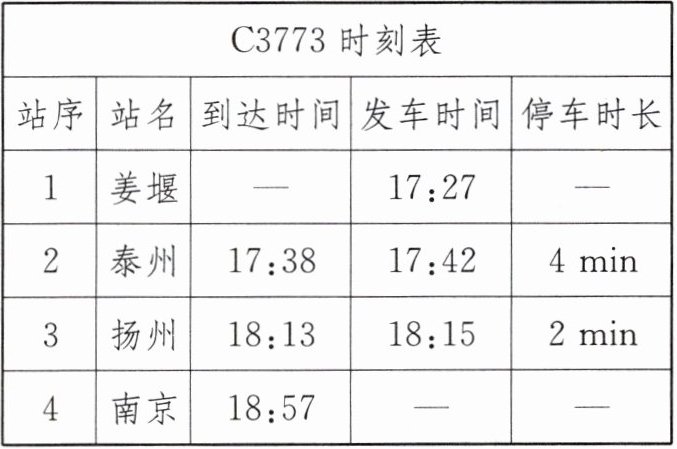
9. 教材P139习题T4·变式 (2025·泰州姜堰区期末)如今,高铁极大地方便了人们的出行,假期在姜堰的小明选择乘坐高铁去南京,他通过12306手机APP查询到C3773次列车的时刻表如表所示.
(1)本次列车从泰州到扬州运行的时间为多少分钟?
(2)姜堰到南京全程约为180 km,列车驶完全程的平均速度是多少千米每小时?
(3)已知列车的长度为200 m,若列车以180 km/h的速度匀速驶过长为1000 m的大桥时,则列车完全通过大桥所用的时间是多少?
|站序|站名|到达时间|发车时间|停车时长|
|1|姜堰|—|17:27|—|
|2|泰州|17:38|17:42|4 min|
|3|扬州|18:13|18:15|2 min|
|4|南京|18:57|—|—|
(1)本次列车从泰州到扬州运行的时间为多少分钟?
(2)姜堰到南京全程约为180 km,列车驶完全程的平均速度是多少千米每小时?
(3)已知列车的长度为200 m,若列车以180 km/h的速度匀速驶过长为1000 m的大桥时,则列车完全通过大桥所用的时间是多少?
|站序|站名|到达时间|发车时间|停车时长|
|1|姜堰|—|17:27|—|
|2|泰州|17:38|17:42|4 min|
|3|扬州|18:13|18:15|2 min|
|4|南京|18:57|—|—|

答案:
(1)31 min
(2)120 km/h
(3)24 s[解析]
(1)泰州的发车时间为 17:42,到达扬州的时间为 18:13,列车从泰州到扬州运行的时间为 31 min.
(2)列车从姜堰到南京运行的时间$t=1.5h$,列车驶完全程的平均速度$v=\frac {s}{t}=\frac {180km}{1.5h}=120km/h$.
(3)列车完全通过大桥行驶的路程$s_{1}=200m+1000m=1200m$,列车完全通过大桥所用的时间$t_{1}=\frac {s_{1}}{v_{1}}=\frac {1200m}{\frac {180}{3.6}m/s}=24s.$
(1)31 min
(2)120 km/h
(3)24 s[解析]
(1)泰州的发车时间为 17:42,到达扬州的时间为 18:13,列车从泰州到扬州运行的时间为 31 min.
(2)列车从姜堰到南京运行的时间$t=1.5h$,列车驶完全程的平均速度$v=\frac {s}{t}=\frac {180km}{1.5h}=120km/h$.
(3)列车完全通过大桥行驶的路程$s_{1}=200m+1000m=1200m$,列车完全通过大桥所用的时间$t_{1}=\frac {s_{1}}{v_{1}}=\frac {1200m}{\frac {180}{3.6}m/s}=24s.$
10. 图示法 某物理兴趣小组利用带有刻度尺的斜面、小车和秒表“测量小车的平均速度”,如图所示,图中显示他们测量过程中的小车在甲、乙、丙三个位置及其对应时间的情形,显示时间的格式是“时:分:秒”.

(1)在测量过程中,
| |甲至乙|乙至丙|甲至丙|
|路程/cm|s_1= 26.0|s_2= 64.0|s_3= 90.0|
|时间/s|t_1= 2|t_2= 4|t_3= 6|

(2)某同学计算甲至丙这个过程的平均速度,采用了下列两种方法计算:
方法1:$v_{3}= \frac {s_{3}}{t_{3}}$;方法2:$v_{3}= (\frac {s_{1}}{t_{1}}+\frac {s_{2}}{t_{2}})×\frac {1}{2}.$
以上两种方法正确的是
(3)要使小车的平均速度增大,下列做法合理的是
A. 换用质量更小的小车
B. 减小斜面的倾角
C. 斜面上铺毛巾
D. 增大斜面的长度
(4)实验中需要多次测量,每次必须让小车从斜面的
(5)若小车过了甲位置才开始计时,则测出的甲、乙段的平均速度会
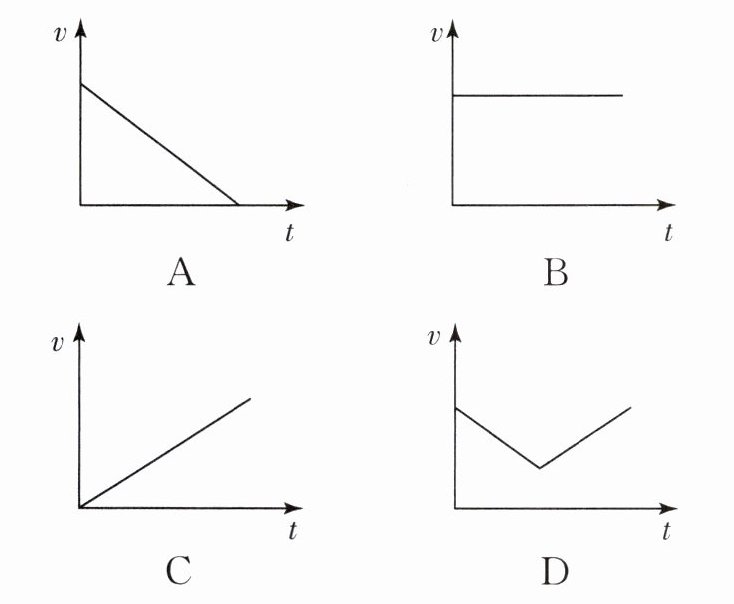
(6)下列四幅图中,能正确反映该小车在斜面上下滑过程中速度随时间变化关系的是
A.
B.
C.
D.
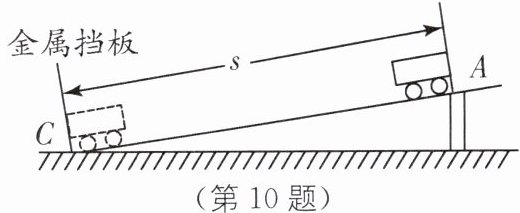
(7)如图所示,同组的小丽测出斜面上A位置到斜面上C位置的距离s和小车从A运动到C位置的时间t,利用测量的数据计算出的平均速度相比小车的实际平均速度

(1)在测量过程中,
时间
(填“路程”或“时间”)更不便测量,为了准确测量,应使斜面的倾角适当 小
(填“大”或“小”)一些.实验数据记录表如下.| |甲至乙|乙至丙|甲至丙|
|路程/cm|s_1= 26.0|s_2= 64.0|s_3= 90.0|
|时间/s|t_1= 2|t_2= 4|t_3= 6|

(2)某同学计算甲至丙这个过程的平均速度,采用了下列两种方法计算:
方法1:$v_{3}= \frac {s_{3}}{t_{3}}$;方法2:$v_{3}= (\frac {s_{1}}{t_{1}}+\frac {s_{2}}{t_{2}})×\frac {1}{2}.$
以上两种方法正确的是
方法 1
(填“方法1”或“方法2”).甲至丙的平均速度是 0.15
m/s.(3)要使小车的平均速度增大,下列做法合理的是
D
.A. 换用质量更小的小车
B. 减小斜面的倾角
C. 斜面上铺毛巾
D. 增大斜面的长度
(4)实验中需要多次测量,每次必须让小车从斜面的
同一位置
由静止开始下滑.(5)若小车过了甲位置才开始计时,则测出的甲、乙段的平均速度会
偏大
;若小车还没有到达丙位置就停止计时,则测出的甲、丙段的平均速度会 偏大
.(填“偏大”或“偏小”)(6)下列四幅图中,能正确反映该小车在斜面上下滑过程中速度随时间变化关系的是
C
.A.
B.
C.
D.

(7)如图所示,同组的小丽测出斜面上A位置到斜面上C位置的距离s和小车从A运动到C位置的时间t,利用测量的数据计算出的平均速度相比小车的实际平均速度
偏大
(填“偏大”“偏小”或“不变”),理由是 测量 s 时,小车的长度测量在内
.
答案:
(1)时间 小
(2)方法 1 0.15
(3)D
(4)同一位置
(5)偏大 偏大
(6)C
(7)偏大 测量 s 时,小车的长度测量在内[解析]
(1)斜面的坡度越大,小车在斜面上运动得越快,时间越短,为了便于测量时间,应使斜面的坡度小一些.
(2)平均速度是用总路程比总时间,即方法 1 正确.甲至丙的平均速度$v_{3}=\frac {s_{3}}{t_{3}}=\frac {90.0cm}{6s}=0.15m/s$.
(3)在路程一定时,要使小车的平均速度增大,需要减小小车下滑的时间,可以通过增大斜面角度、在更光滑的斜面上实验来实现.小车下滑速度与小车的质量无关,A 不符合题意;减小斜面的倾角,下滑的速度减小,B 不符合题意;斜面上铺毛巾,小车的速度减小,C 不符合题意;增大斜面的长度,由于小车下滑过程中做加速运动,所以速度增大,D 符合题意.
(4)多次测量,为了减小实验误差,应控制每次实验的条件相同,即每次必须让小车从斜面的同一位置由静止开始下滑.
(5)小车过了甲位置才开始计时,导致测量甲、乙段的时间偏小,根据$v=\frac {s}{t}$可知,速度偏大.若小车还没有到达丙位置就停止计时,导致测量甲、丙段的时间偏小,根据$v=\frac {s}{t}$可知,速度偏大.
(6)小车在斜面上做加速运动,即速度越来越快,C 符合题意.
(7)由图可知,测量距离时,将小车的长度也计算在内,导致来测量的距离 s 偏大,根据$v=\frac {s}{t}$可知,利用测量的数据计算出的平均速度相比小车的实际平均速度偏大.名师点评 在平均速度的测量中,依据公式$v=\frac {s}{t}$,时间t 的测量值偏大会导致速度v 的计算结果偏小,反之则偏大;而路程 s 的测量值偏大将引起速度v 的计算结果偏大,反之偏小.
(1)时间 小
(2)方法 1 0.15
(3)D
(4)同一位置
(5)偏大 偏大
(6)C
(7)偏大 测量 s 时,小车的长度测量在内[解析]
(1)斜面的坡度越大,小车在斜面上运动得越快,时间越短,为了便于测量时间,应使斜面的坡度小一些.
(2)平均速度是用总路程比总时间,即方法 1 正确.甲至丙的平均速度$v_{3}=\frac {s_{3}}{t_{3}}=\frac {90.0cm}{6s}=0.15m/s$.
(3)在路程一定时,要使小车的平均速度增大,需要减小小车下滑的时间,可以通过增大斜面角度、在更光滑的斜面上实验来实现.小车下滑速度与小车的质量无关,A 不符合题意;减小斜面的倾角,下滑的速度减小,B 不符合题意;斜面上铺毛巾,小车的速度减小,C 不符合题意;增大斜面的长度,由于小车下滑过程中做加速运动,所以速度增大,D 符合题意.
(4)多次测量,为了减小实验误差,应控制每次实验的条件相同,即每次必须让小车从斜面的同一位置由静止开始下滑.
(5)小车过了甲位置才开始计时,导致测量甲、乙段的时间偏小,根据$v=\frac {s}{t}$可知,速度偏大.若小车还没有到达丙位置就停止计时,导致测量甲、丙段的时间偏小,根据$v=\frac {s}{t}$可知,速度偏大.
(6)小车在斜面上做加速运动,即速度越来越快,C 符合题意.
(7)由图可知,测量距离时,将小车的长度也计算在内,导致来测量的距离 s 偏大,根据$v=\frac {s}{t}$可知,利用测量的数据计算出的平均速度相比小车的实际平均速度偏大.名师点评 在平均速度的测量中,依据公式$v=\frac {s}{t}$,时间t 的测量值偏大会导致速度v 的计算结果偏小,反之则偏大;而路程 s 的测量值偏大将引起速度v 的计算结果偏大,反之偏小.
查看更多完整答案,请扫码查看


