第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
5.(2024·宿迁泗阳县期末)甲、乙两小车同时沿同一直线运动,它们的 s-t 图像如图所示.经过5s,甲、乙两小车正好相遇,求:
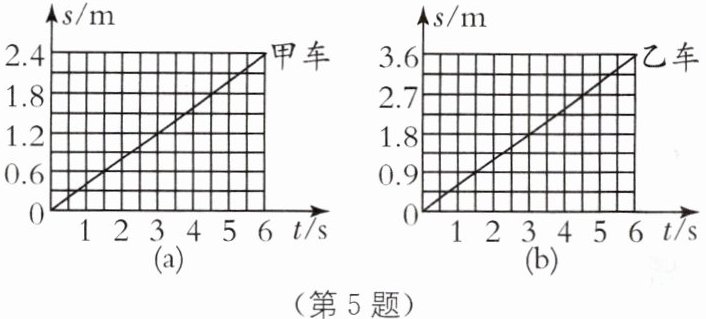
(1)小车甲的速度;
(2)经过5s时,乙车通过的路程;
(3)开始计时时,甲、乙两小车之间的距离.

(1)小车甲的速度;
(2)经过5s时,乙车通过的路程;
(3)开始计时时,甲、乙两小车之间的距离.
答案:
5.
(1)0.4 m/s
(2)3 m
(3)5 m或1 m
[解析]
(1)由题图(a)可知,甲车行驶2.4 m,用时6 s,则甲车速度$v_{甲}=\frac {s_{甲}}{t_{甲}}=\frac {2.4m}{6s}=0.4m/s$.
(2)由题图(b)可知,乙车行驶3.6 m,用时6 s,则乙车速度$v_{乙}=\frac {s_{乙}}{t_{乙}}=\frac {3.6m}{6s}=$$0.6m/s$,经过5 s,乙车通过的路程$s_{乙}'=v_{乙}t_{乙}'=0.6m/s×$$5s=3m$.
(3)经过5 s,甲车通过的路程$s_{甲}'=v_{甲}t_{甲}'=$$0.4m/s×5s=2m$.经过5 s,甲、乙两小车正好相遇,如果甲、乙两小车相向而行,则开始计时时,甲、乙两小车之间的距离$s_{甲乙}=s_{甲}'+s_{乙}'=2m+3m=5m$;如果甲、乙两小车同向而行,由于乙车速度更快,所以应该为乙车追击甲车,否则甲车不可能追上乙车,则开始计时时,甲、乙两小车之间的距离$s_{甲乙}'=s_{乙}'-s_{甲}'=3m-2m=1m.$
(1)0.4 m/s
(2)3 m
(3)5 m或1 m
[解析]
(1)由题图(a)可知,甲车行驶2.4 m,用时6 s,则甲车速度$v_{甲}=\frac {s_{甲}}{t_{甲}}=\frac {2.4m}{6s}=0.4m/s$.
(2)由题图(b)可知,乙车行驶3.6 m,用时6 s,则乙车速度$v_{乙}=\frac {s_{乙}}{t_{乙}}=\frac {3.6m}{6s}=$$0.6m/s$,经过5 s,乙车通过的路程$s_{乙}'=v_{乙}t_{乙}'=0.6m/s×$$5s=3m$.
(3)经过5 s,甲车通过的路程$s_{甲}'=v_{甲}t_{甲}'=$$0.4m/s×5s=2m$.经过5 s,甲、乙两小车正好相遇,如果甲、乙两小车相向而行,则开始计时时,甲、乙两小车之间的距离$s_{甲乙}=s_{甲}'+s_{乙}'=2m+3m=5m$;如果甲、乙两小车同向而行,由于乙车速度更快,所以应该为乙车追击甲车,否则甲车不可能追上乙车,则开始计时时,甲、乙两小车之间的距离$s_{甲乙}'=s_{乙}'-s_{甲}'=3m-2m=1m.$
6.新情境 驾驶员的驾车安全与健康 一辆小车以 25 m/s的速度匀速行驶,司机突然发现前方有紧急情况以后过0.6s开始刹车,又经过4.4s滑行52m后,车停止运动.问:
(1)从发现情况到开始刹车,小车运动的距离是多少?
(2)在滑行 52 m 的过程中的平均速度是多少?(小数点后保留一位有效数字)
(3)从发现情况到车停止运动的平均速度为多少?
(1)从发现情况到开始刹车,小车运动的距离是多少?
(2)在滑行 52 m 的过程中的平均速度是多少?(小数点后保留一位有效数字)
(3)从发现情况到车停止运动的平均速度为多少?
答案:
6.
(1)15 m
(2)11.8 m/s
(3)13.4 m/s
[解析]
(1)由$v=\frac {s}{t}$可得,从发现情况到开始刹车,汽车行驶的路程$s_{1}=v_{1}t_{1}=25m/s×0.6s=15m$.
(2)汽车在滑行52 m的过程中的平均速度$v_{2}=\frac {s_{2}}{t_{2}}=$$\frac {52m}{4.4s}\approx 11.8m/s$.
(3)从发现情况到车停止行驶的路程$s_{总}=s_{1}+s_{2}=15m+$$52m=67m$,从发现情况到车停止行驶的时间$t=t_{1}+t_{2}=$$0.6s+4.4s=5s$,车的平均速度$v=\frac {s_{总}}{t}=\frac {67m}{5s}=$$13.4m/s.$
(1)15 m
(2)11.8 m/s
(3)13.4 m/s
[解析]
(1)由$v=\frac {s}{t}$可得,从发现情况到开始刹车,汽车行驶的路程$s_{1}=v_{1}t_{1}=25m/s×0.6s=15m$.
(2)汽车在滑行52 m的过程中的平均速度$v_{2}=\frac {s_{2}}{t_{2}}=$$\frac {52m}{4.4s}\approx 11.8m/s$.
(3)从发现情况到车停止行驶的路程$s_{总}=s_{1}+s_{2}=15m+$$52m=67m$,从发现情况到车停止行驶的时间$t=t_{1}+t_{2}=$$0.6s+4.4s=5s$,车的平均速度$v=\frac {s_{总}}{t}=\frac {67m}{5s}=$$13.4m/s.$
7.(2024·泰州海陵区期末)国庆节期间,小华和父母乘坐家庭小汽车外出旅行,途中小华利用手机进行以下两种实践.

(1)当汽车到达图甲标识牌位置时,小华立即按下手机上秒表开始计时,到达图乙标识牌时立即停止计时,记录时间为48 min,通过计算粗略判断小汽车在该过程是否超速.
(2)当他们即将下高速时,小华听到导航中说"前方进入匝道,限速 40",他运用"手机物理工坊"的"声学秒表",记录了汽车前后轮撞击减速带时两次"咚"声的时间差,如图丙所示.他通过手机查找该型号汽车前后轮间距为2850 mm,通过计算估测小汽车在匝道行驶时是否超速(声音在汽车中传播的时间不计).

(1)当汽车到达图甲标识牌位置时,小华立即按下手机上秒表开始计时,到达图乙标识牌时立即停止计时,记录时间为48 min,通过计算粗略判断小汽车在该过程是否超速.
(2)当他们即将下高速时,小华听到导航中说"前方进入匝道,限速 40",他运用"手机物理工坊"的"声学秒表",记录了汽车前后轮撞击减速带时两次"咚"声的时间差,如图丙所示.他通过手机查找该型号汽车前后轮间距为2850 mm,通过计算估测小汽车在匝道行驶时是否超速(声音在汽车中传播的时间不计).
答案:
7.
(1)没有超速
(2)没有超速
[解析]
(1)测速区间的速度$v=\frac {s}{t}=\frac {66km}{\frac {48}{60}h}=82.5km/h<$$100km/h$,所以小汽车在该过程没有超速.
(2)小汽车在匝道行驶速度$v'=\frac {s'}{t'}=\frac {2.85m}{0.3s}=9.5m/s=34.2km/h<$$40km/h$,所以小汽车在匝道行驶时没有超速.
(1)没有超速
(2)没有超速
[解析]
(1)测速区间的速度$v=\frac {s}{t}=\frac {66km}{\frac {48}{60}h}=82.5km/h<$$100km/h$,所以小汽车在该过程没有超速.
(2)小汽车在匝道行驶速度$v'=\frac {s'}{t'}=\frac {2.85m}{0.3s}=9.5m/s=34.2km/h<$$40km/h$,所以小汽车在匝道行驶时没有超速.
8.(2024·南京鼓楼区期末)我国自主建设、独立运行的北斗卫星导航系统可提供高精度的定位、导航和授时服务,手机地图 APP 就采用了该导航系统,为日常出行提供服务.节假日,小明和小华外出游玩,他们从宝船遗址公园公交站出发前往江苏科技馆,小明通过地图 APP 搜索了出行方案:
|方案一(公共交通)|方案二(骑行)|
|47路公交车 4站 6分钟 步行 420米 7分钟|12分钟 2.3千米|
两人商量后,小明选择方案一,小华选择方案二.上午9:30,小明和小华同时出发.
(1)小华实际到达科技馆的时间为9:40,则骑行时的平均速度为多少千米每小时?
(2)小明下车后,9:37 开始步行,若按照1.4 m/s 的速度步行1 min 后开始慢跑,最终和小华同时达到科技馆,则慢跑阶段的平均速度为多少米每秒?
|方案一(公共交通)|方案二(骑行)|
|47路公交车 4站 6分钟 步行 420米 7分钟|12分钟 2.3千米|
两人商量后,小明选择方案一,小华选择方案二.上午9:30,小明和小华同时出发.
(1)小华实际到达科技馆的时间为9:40,则骑行时的平均速度为多少千米每小时?
(2)小明下车后,9:37 开始步行,若按照1.4 m/s 的速度步行1 min 后开始慢跑,最终和小华同时达到科技馆,则慢跑阶段的平均速度为多少米每秒?
答案:
8.
(1)13.8 km/h
(2)2.8 m/s [解析]
(1)小华选择方案二,上午9:30出发,小华实际到达科技馆的时间为9:40,小华所用时间$t=10min$,小华骑行的路程是2.3 km,所以小华骑行时的平均速度$v=\frac {s}{t}=\frac {2.3km}{10×\frac {1}{60}h}=$$13.8km/h$.
(2)小明下车后,9:37开始步行,按照1.4 m/s的速度步行1 min,即小明9:38开始慢跑,最终9:40到达科技馆,所以小明慢跑的时间$t_{慢}=2min$,小明步行的路程$s_{步}=v_{步}t_{步}=1.4m/s×1×60s=84m$,小明慢跑的路程$s_{慢}=420m-84m=336m$,小明慢跑的平均速度$v_{慢}=\frac {s_{慢}}{t_{慢}}=\frac {336m}{2×60s}=2.8m/s.$
(1)13.8 km/h
(2)2.8 m/s [解析]
(1)小华选择方案二,上午9:30出发,小华实际到达科技馆的时间为9:40,小华所用时间$t=10min$,小华骑行的路程是2.3 km,所以小华骑行时的平均速度$v=\frac {s}{t}=\frac {2.3km}{10×\frac {1}{60}h}=$$13.8km/h$.
(2)小明下车后,9:37开始步行,按照1.4 m/s的速度步行1 min,即小明9:38开始慢跑,最终9:40到达科技馆,所以小明慢跑的时间$t_{慢}=2min$,小明步行的路程$s_{步}=v_{步}t_{步}=1.4m/s×1×60s=84m$,小明慢跑的路程$s_{慢}=420m-84m=336m$,小明慢跑的平均速度$v_{慢}=\frac {s_{慢}}{t_{慢}}=\frac {336m}{2×60s}=2.8m/s.$
查看更多完整答案,请扫码查看


