《2025年实验班提优训练九年级数学上册苏科版》

1. (2024·无锡中考)已知圆锥的底面圆半径为 3,母线长为 4,则圆锥的侧面积为(B).
A.6π
B.12π
C.15π
D.24π

答案： B

2. (2024·广州中考)如图,圆锥的侧面展开图是一个圆心角为 72°的扇形,若扇形的半径 l 是 5,则该圆锥的体积是(D).
A.$\frac {3\sqrt {11}}{8}\pi$
B.$\frac {\sqrt {11}}{8}\pi$
C.$2\sqrt {6}\pi$
D.$\frac {2\sqrt {6}}{3}\pi$
]

答案： D　[解析]由题意得圆锥的底面圆的周长为$\frac{72π×5}{180}=2π$，故圆锥的底面圆的半径为$\frac{2π}{2π}=1$，
　所以圆锥的高为$\sqrt{5^{2}-1^{2}}=2\sqrt{6}$，
　所以该圆锥的体积为$\frac{1}{3}π×1^{2}×2\sqrt{6}=\frac{2\sqrt{6}}{3}π$。
　故选D。

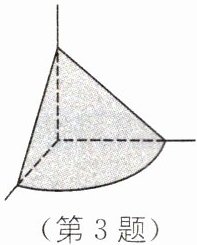
3. 传统文化 《九章算术》《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题：“今有委米依垣内角,下周八尺,高五尺,问积及为米几何?”译文:屋内墙角处的米堆为一个圆锥的四分之一(如图),米堆底部的弧长为8尺,米堆的高为5尺,那么这个米堆遮挡的墙面面积为(A).

A.$\frac {80}{\pi}$平方尺
B.$\frac {160}{\pi}$平方尺
C.$\frac {128}{\pi}$平方尺
D.45π平方尺

答案： A　[解析]设圆锥的底面半径为r尺，由米堆底部的弧长为8尺，可得$\frac{1}{4}×2πr=8$，解得$r=\frac{16}{π}$，
∴$2×\frac{1}{2}×\frac{16}{π}×5=\frac{80}{π}$(平方尺)，
∴这个米堆遮挡的墙面面积为$\frac{80}{π}$平方尺。故选A

4. (2024·通辽中考)如图,为便于研究圆锥与扇形的关系,小方同学利用扇形纸片恰好围成一个底面半径为5 cm,母线长为12 cm 的圆锥的侧面,那么这个扇形纸片的面积是______$cm^{2}$(结果用含π的式子表示).
]

60π

答案： 60π

5. (2024·扬州中考)若用半径为 10 cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥底面圆的半径为5cm.

答案： 5　[解析]由题意可知圆锥的底面周长为10πcm，
　则圆锥底面圆的半径为$\frac{10π}{2π}=5$(cm)。

6. (2024·徐州中考)将圆锥的侧面沿一条母线剪开后展平,所得扇形的面积为$4\pi cm^{2}$,圆心角θ为90°,圆锥的底面圆的半径为______1cm.

答案： 1cm　[解析]设扇形的半径为Rcm，弧长为lcm，
　由题意，得$\frac{90π×R^{2}}{360}=4π$，解得$R=4$(负值舍去)，
　则$\frac{1}{2}l×4=4π$，解得$l=2π$，
∴圆锥的底面圆的半径为$2π÷2π=1$(cm)。
　归纳总结　本题考查了圆锥的计算，圆锥的侧面展开图为扇形，这个扇形的弧长等于圆锥底面圆的周长，扇形的半径等于圆锥的母线长。

7. (南京二十九中特长生)一个圆锥,过高的截面为等边三角形,求展开后扇形的圆心角.
]

答案： 设圆锥的母线长l，则底面直径为l，
　设侧面展开图圆心角为$θ^{\circ}$，则$\frac{θπl}{180}=πl$，
∴$θ=180$，
∴展开后扇形的圆心角为$180^{\circ}$。

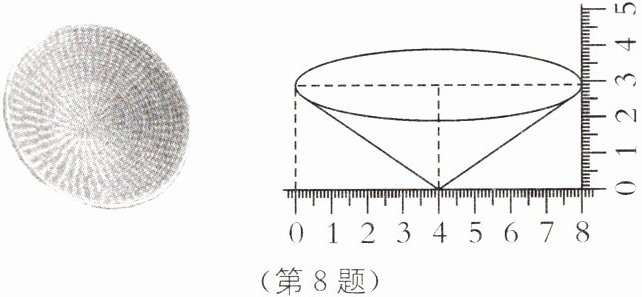
8. (2025·镇江句容期中)草锅盖,又名盖顶,是一种以牛筋草、江边草和斑茅草为原材料进行编织缠绕的云南特有的传统草编工艺品.某兴趣小组根据草锅盖的特征制作了一个圆锥模型,并用测量工具测量其尺寸,如图所示,由图中的数据可知圆锥模型的侧面积为(B).

A.$16\pi cm^{2}$
B.$20\pi cm^{2}$
C.$24\pi cm^{2}$
D.$25\pi cm^{2}$

答案： B　[解析]由图中的数据可知圆锥的底面直径为8cm，圆锥的高为3cm，
　则圆锥的母线长为$\sqrt{4^{2}+3^{2}}=5$(cm)，
∴圆锥模型的侧面积为$\frac{1}{2}π×8×5=20π$(cm²)。
　故选B。

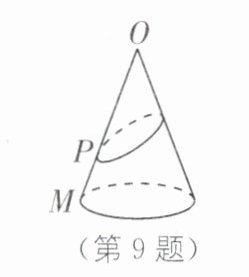
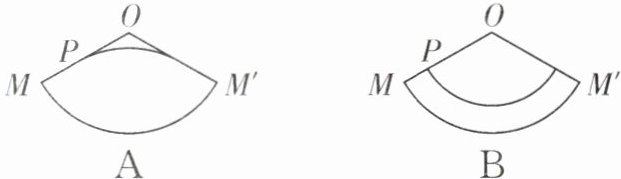
9. 已知 O 为圆锥的顶点,M 为圆锥底面上一点,点 P 在 OM 上.一只蜗牛从点 P 出发,绕圆锥侧面爬行,回到点 P 时所爬过的最短路线的痕迹如图所示,若沿 OM 将圆锥侧面剪开并展开,所得侧面展开图是(D).
]

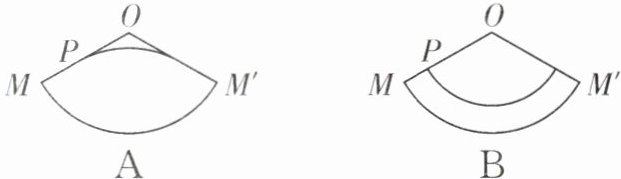
答案： D