第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
1.(2025·无锡外国语学校期中)下列说法中正确的是(
A.弦是直径
B.弧是半圆
C.半圆是圆中最长的弧
D.直径是圆中最长的弦
D
).A.弦是直径
B.弧是半圆
C.半圆是圆中最长的弧
D.直径是圆中最长的弦
答案:
D [解析]A.错误,直径是弦,弦不一定是直径;
B.错误,弧是圆上两点间的部分;
C.错误,优弧大于半圆;
D.正确,直径是圆中最长的弦.故选D.
B.错误,弧是圆上两点间的部分;
C.错误,优弧大于半圆;
D.正确,直径是圆中最长的弦.故选D.
2.(2025·镇江期中)嘉嘉在半径为5 cm 的$\odot O$中测量弦AB 的长度,则下列测量结果中一定错误的是(
A.4 cm
B.5 cm
C.8 cm
D.11 cm
D
).A.4 cm
B.5 cm
C.8 cm
D.11 cm
答案:
D [解析]
∵半径为5cm的圆,直径为10cm,
∴在半径为5的圆中测量弦AB的长度,AB的取值范围是0cm<AB≤10cm,
∴弦AB的长度可以是4cm,5cm,8cm,不可能为11cm.故选D.
∵半径为5cm的圆,直径为10cm,
∴在半径为5的圆中测量弦AB的长度,AB的取值范围是0cm<AB≤10cm,
∴弦AB的长度可以是4cm,5cm,8cm,不可能为11cm.故选D.
3. 实验班原创 如图,A、B、C 是$\odot O$上三点,$\angle A= 78^{\circ }$,$\angle C= 62^{\circ }$,则$\angle AOC$的大小为______.


80°
答案:
80° [解析]连接OB.
∵OA=OB,
∴∠OBA=∠A=78°,
∴∠AOB=180°−∠A−∠OBA=180°−78°−78°=24°.
∵OB=OC,
∴∠OBC=∠C=62°,
∴∠BOC=180°−∠OBC−∠C=180°−62°−62°=56°,
∴∠AOC=∠AOB+∠BOC=24°+56°=80°.
∵OA=OB,
∴∠OBA=∠A=78°,
∴∠AOB=180°−∠A−∠OBA=180°−78°−78°=24°.
∵OB=OC,
∴∠OBC=∠C=62°,
∴∠BOC=180°−∠OBC−∠C=180°−62°−62°=56°,
∴∠AOC=∠AOB+∠BOC=24°+56°=80°.
4. 教材 P41 思考与探索·变式 如图,AB 为$\odot O$的直径,CD 是$\odot O$的弦,AB、CD 的延长线交于点 E,已知$AB= 2DE$,$\angle AEC= 20^{\circ }$,求$\angle AOC$的度数.
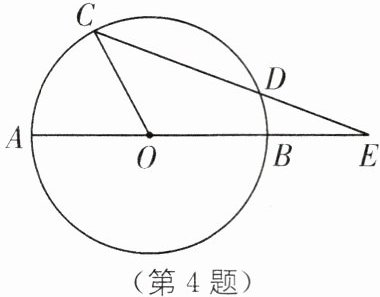

答案:
连接OD.
∵AB=2DE,而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°.又OC=OD,
∴∠C=∠CDO=40°,
∴∠AOC=∠C+∠E=40°+20°=60°.
∵AB=2DE,而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°.又OC=OD,
∴∠C=∠CDO=40°,
∴∠AOC=∠C+∠E=40°+20°=60°.
5.(2025·常州期中)如图,点 A、B、C 是$\odot O$上不重合的三点,则下列结论一定正确的是( ).
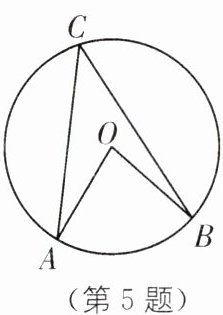
A.$\angle AOB= \angle A+\angle B$
B.$\angle AOB= 2(\angle A+\angle B)$
C.$\angle AOB= 90^{\circ }-(\angle A+\angle B)$
D.$\angle AOB= 180^{\circ }-2(\angle A+\angle B)$

A.$\angle AOB= \angle A+\angle B$
B.$\angle AOB= 2(\angle A+\angle B)$
C.$\angle AOB= 90^{\circ }-(\angle A+\angle B)$
D.$\angle AOB= 180^{\circ }-2(\angle A+\angle B)$
答案:
B [解析]如图,连接CO并延长交⊙O于点D.

∵OA=OB=OC,
∴∠A=∠OCA,∠B=∠OCB,
∴∠AOD=∠A+∠OCA=2∠A,∠BOD=∠B+∠OCB=2∠B,
∴∠AOD+∠BOD=2(∠A+∠B),
即∠AOB=2(∠A+∠B).故选B
B [解析]如图,连接CO并延长交⊙O于点D.

∵OA=OB=OC,
∴∠A=∠OCA,∠B=∠OCB,
∴∠AOD=∠A+∠OCA=2∠A,∠BOD=∠B+∠OCB=2∠B,
∴∠AOD+∠BOD=2(∠A+∠B),
即∠AOB=2(∠A+∠B).故选B
6. 新情境 构建模型 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时捕捉. 把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,$\angle ABC= 90^{\circ }$,点 M、N 分别在射线 BA、BC 上,MN 长度始终保持不变,$MN= 4$,E 为 MN 的中点,点 D 到 BA、BC 的距离分别为 3 和 2,在此滑动过程中,猫与老鼠的距离 DE 的最小值为(
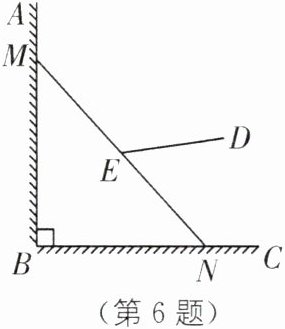
A.$2\sqrt {5}-2$
B.$\sqrt {13}-1$
C.$\sqrt {13}-2$
D.$\sqrt {13}-3$
C
).
A.$2\sqrt {5}-2$
B.$\sqrt {13}-1$
C.$\sqrt {13}-2$
D.$\sqrt {13}-3$
答案:
C [解析]连接BE、BD,
由勾股定理,得BD=$\sqrt{3^2+2^2}$=$\sqrt{13}$.
∵在Rt△MBN中,点E是MN的中点,MN=4,
∴BE=$\frac{1}{2}$MN=2,
∴点E的运动轨迹是以点B为圆心,2为半径的弧,
∴当点E落在线段BD上时,DE的值最小,
∴DE的最小值为$\sqrt{13}$−2.故选C.
易错警示 注意区分“两点之间线段最短”和“垂线段最短”的不同,前者是两个点之间,后者是点与线之间,并且必须垂直.
由勾股定理,得BD=$\sqrt{3^2+2^2}$=$\sqrt{13}$.
∵在Rt△MBN中,点E是MN的中点,MN=4,
∴BE=$\frac{1}{2}$MN=2,
∴点E的运动轨迹是以点B为圆心,2为半径的弧,
∴当点E落在线段BD上时,DE的值最小,
∴DE的最小值为$\sqrt{13}$−2.故选C.
易错警示 注意区分“两点之间线段最短”和“垂线段最短”的不同,前者是两个点之间,后者是点与线之间,并且必须垂直.
7.(2025·南京鼓楼区期末)平面内 A、B、C、D、E 五个点如图,过点
A、E、C
所作的圆的半径最大.(从中选填三个点)
答案:
A、E、C
8. 教材 P43 习题 T8·变式(2025·泰州靖江期中改编)如图,$\odot O的直径AB= 12$,半径$OC\perp AB$,D 为弧 BC 上一动点(不包括 B、C 两点),$DE\perp OC$,$DF\perp AB$,垂足分别为 E、F,求 EF 的长.


答案:
连接OD,
∵⊙O的直径AB=12,
∴圆的半径OD=12÷2=6.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=6.
∵⊙O的直径AB=12,
∴圆的半径OD=12÷2=6.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=6.
查看更多完整答案,请扫码查看


